【题目】如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=34°,∠AEB=72°.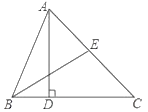
(1)求∠CAD和∠BAD的度数;
(2)若点F为线段BC上任意一点,当△EFC为直角三角形时,试求∠BEF的度数.
参考答案:
【答案】
(1)解:∵BE为△ABC的角平分线,
∴∠CBE=∠EBA=34°,
∵∠AEB=∠CBE+∠C,
∴∠C=72°﹣34°=38°,
∵AD为△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=52°,
∠BAD=90°-∠ABD=90°-68°=22°
(2)解:当∠EFC=90°时,∠BEF=90°﹣∠CBE=56°,
当∠FEC=90°时,∠BEF=180°-72°﹣90°=18°
【解析】(1)由BE为∠ABC的平分线,得出∠BAD=22°,再求出∠C,得出∠CAD=52°,即可得出结论;
(2)分两种情况:①当∠EFC=90°时;②当∠FEC=90°时;由角的互余关系和三角形的外角性质即可求出∠BEF的度数.
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线),还要掌握垂线的性质(垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)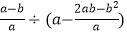 ;
;
(2)(﹣4ab3)(﹣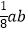 )﹣(
)﹣(  )2 .
)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2(x-1)>3x-4的非负整数解为______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的是( )
A.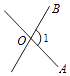
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1-t,y=2-3t,那么用含x的代数式表示y为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α与∠β同旁内角,且∠α=50°时,则∠β的度数为( )
A. 50° B. 130° C. 50°或130° D. 无法确定
相关试题

