【题目】等腰Rt△ABC中,CA=CB,∠ACB=90°,点O是AB的中点.
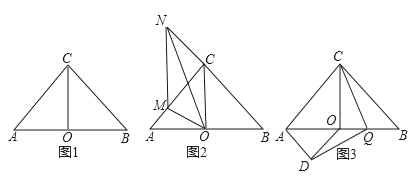
(1)如图1,求证:CO=BO;
(2)如图2,点M在边AC上,点N在边BC延长线上,MN﹣AM=CN,求∠MON的度数;
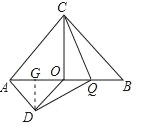
(3)如图3,AD∥BC,OD∥AC,AD与OD交于点D,Q是OB的中点,连接CQ、DQ,试判断线段CQ与DQ的关系,并给出证明.
参考答案:
【答案】(1)详见解析;(2)45°;(3)QC=QD,QC⊥QD,理由详见解析.
【解析】
(1)根据等腰三角形的三线合一证明;
(2)在线段BC上取点H,使CH=AM,连接OH,分别证明△AOM≌△COH和△MON≌△HON,根据全等三角形的性质计算即可;
(3)作DG⊥AO于G,证明△COQ≌△QGD,根据全等三角形的性质,垂直的定义证明.
(1)∵∠ACB=90°,AO=BO,
∴CO=![]() AB=BO;
AB=BO;
(2)在线段BC上取点H,使CH=AM,连接OH,如图所示
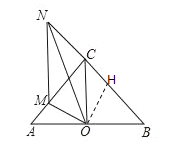
∵∠ACB=90°,AO=BO,
∴∠A=∠B=45°,∠ACO=∠BCO=45°,
在△AOM和△COH中,
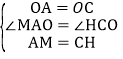 ,
,
∴△AOM≌△COH(SAS)
∴OM=OH,
∵MN﹣AM=CN,
∴NM=NH,
在△MON和△HON中,
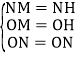 ,
,
∴△MON≌△HON(SSS),
∴∠MON=∠HON,
∴∠MON=∠AOM+∠CON,
∴∠MON=![]() ∠AOC=45°;
∠AOC=45°;
(3)QC=QD,QC⊥QD,
理由如下:作DG⊥AO于G,
∵AD∥BC,
∴∠OAD=∠B=45°,
∵OD∥AC,
∴∠AOD=∠OAC=45°,
∴DA=DO,又DG⊥AO,
∴DG=AG=GO=![]() OA,
OA,
∵Q是OB的中点,
∴OQ=BQ=![]() OB,
OB,
∴DG=OQ,GQ=OC,
在△COQ和△QGD中,
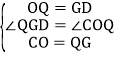 ,
,
∴△COQ≌△QGD(SAS),
∴QC=QD,∠GQD=∠OCQ,
∵∠OCQ+∠CQO=90°,
∴∠GQD+∠CQO=90°,即∠CQD=90°,
∴QC⊥QD,
则QC=QD,QC⊥QD.
-
科目: 来源: 题型:
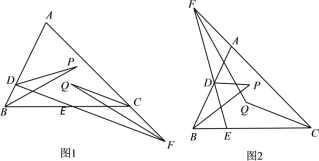
查看答案和解析>>【题目】已知D、E分别为△ABC中AB、BC上的动点,直线DE与直线AC相交于F,∠ADE的平分线与∠B的平分线相交于P,∠ACB的平分线与∠F的平分线相交于Q.
(1)如图1,当F在AC的延长线上时,求∠P与∠Q之间的数量关系;
(2)如图2,当F在AC的反向延长线上时,求∠P与∠Q之间的数量关系(用等式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在“清明小假期”举行促销活动,设立了一个可以自由转动的转盘进行摇奖活动,并规定顾客每购买200元商品,就可以获得一次转动转盘的机会,小明根据活动情况绘制了一个扇形统计图,如图所示.
(1)求每转动一次转盘所获得购物券金额的平均数;
(2)小明做了一次实验,他转了200次转盘,总共获得5800元购物券,他平均每转动一次转盘获得的购物券是多少元?
(3)请你说明上述两个结果为什么有差别?

-
科目: 来源: 题型:
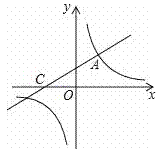
查看答案和解析>>【题目】如图,直线
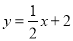 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C. (1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
-
科目: 来源: 题型:
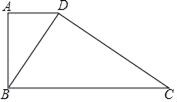
查看答案和解析>>【题目】已知四边形ABCD中,∠BAD=∠BDC=90°,BD2=ADBC.
(1)求证:AD∥BC;
(2)过点A作AE∥CD交BC于点E.请完善图形并求证:CD2=BEBC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有两个可以自由转动的均匀转盘A、B,转盘A被分为3等份,分别标有1、2、3三个数字;转盘B被分为4等份,分别标有3、4、5、6四个数字;有人为甲、乙两人设计了一个游戏规则:自由转动转盘A和B,转盘停止后,指针各指向一个数字(若指针恰好停在分界线上时,当作指向右边的数字),将指针所指的两个数字相加,如果和为6,那么甲获胜,否则乙获胜。

请你用概率的有关知识进行说明,这个游戏规则是否公平?如果不公平,那么谁获胜的可能性大些?
-
科目: 来源: 题型:
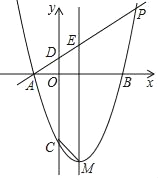
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=1,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.
(1)求点A的坐标和抛物线的表达式;
(2)当AE:EP=1:2时,求点E的坐标;
(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t的值.
相关试题

