【题目】已知∠AOB=45°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,则△P1O P2是( )
A.含30°角的直角三角形
B.顶角是30°的等腰三角形
C.等边三角形
D.等腰直角三角形
参考答案:
【答案】D
【解析】解:∵P1与点P关于OA对称, ∴OP1=OP,∠P1OA=∠POA,
∵点P2与点P关于OB对称
∴OP2=OP,∠P2OB=∠POB
∴OP2=OP1 ,
∠P1OP2=∠P1OP+∠P2OP=2(∠POA+∠POB)=90°
故选(D)
根据轴对称的性质即可判断.
-
科目: 来源: 题型:
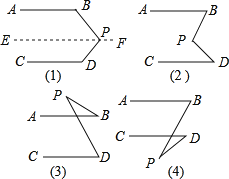
查看答案和解析>>【题目】如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,不需要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m是方程2x2﹣3x﹣1=0的一个根,则6m2﹣9m+2016的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2是关于x的一元二次方程kx2+(k2﹣2)x+2k+4=0的一个根,则k的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1的⊙P的圆心在抛物线y=﹣x2+4x﹣3上运动,当⊙P在x轴相切时,圆心P的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,AB=AC,∠A=50°,则∠B= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x3y﹣4xy= .
相关试题

