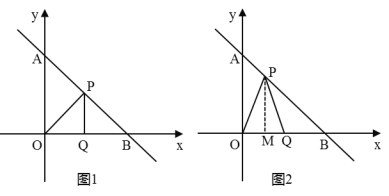
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,动点
两点,动点![]() 在线段
在线段![]() 上移动(与
上移动(与![]() 不重合),以
不重合),以![]() 为顶点作
为顶点作![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)求证:![]() .
.
(3)是否存在点![]() 使得
使得![]() 是等腰三角形?若存在,请直接写出点
是等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析;(3)存在,
;(2)见解析;(3)存在,![]() 或
或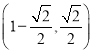
【解析】
(1)令x=0,即可得到点A坐标,令y=0,即可得到点B坐标;
(2)由(1)可知△AOB是等腰直角三角形,再根据三角形的外角的性质即可得到∠OPQ+∠BPQ=∠AOP+∠OAP,结合![]() 即可证明;
即可证明;
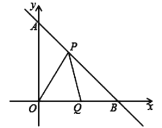
(3)分两种情况讨论,①如图1,当∠OPQ=45°为底角时,得到∠PQO=90°,PQ=OQ,设P(a,a),代入y=-x+1中即可求出P的坐标;②如图2,当∠OPQ=45°为顶角时,根据(2)中结论证明△OAP≌△PBQ(AAS),得到AO=BP=1,利用锐角三角形函数求出PM,OM即可解答.
解:(1)对于y=-x+1,
当x=0时,y=1,当y=0时,x=1,
∴![]()
(2)∵![]() ,
,
∴OA=OB=1,
∴△AOB是等腰直角三角形,
∴∠OAB=∠OBA=45°,
∵∠OPB是△AOP的外角,
∴∠OPB=∠AOP+∠OAP,即∠OPQ+∠BPQ=∠AOP+∠OAP,
又∵![]() ,
,
∴![]() ;
;
(3)存在,
①如图1,当∠OPQ=45°为底角时,
则∠OPQ=∠POQ=45°,
∴∠PQO=90°,PQ=OQ,
设P(a,a),代入y=-x+1中得,a=-a+1,解得:![]() ,
,
∴![]()
②如图2,当∠OPQ=45°为顶角时,过点P作PM⊥OB于点M,
则OP=PQ,
又∵∠OAP=∠PBQ=45°,∠AOP=∠BPQ,
∴△OAP≌△PBQ(AAS),
∴AO=BP=1,
∵∠PBM=45°,∠PMB=90°,
∴PM=BM=![]() ,
,
∴OM=![]() ,
,
∴P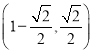
综上所述,点P的坐标为![]() 或
或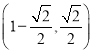 .
.