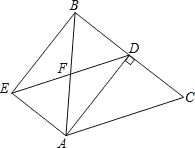
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
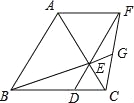
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
【答案】①②③④.
【解析】
试题分析:①由△ABC是等边三角形,可得AB=AC=BC,∠BAC=∠ACB=60°,再因DE=DC,可判定△DEC是等边三角形,所以ED=EC=DC,∠DEC=∠AEF=60°,
因EF=AE,所以△AEF是等边三角形,所以AF=AE,∠EAF=60°,在△ABE和△ACF中,AB=AC,∠BAE=∠CAF,AE=AF ,可判定△ABE≌△ACF,故①正确.②由∠ABC=∠FDC,可得AB∥DF,再因∠EAF=∠ACB=60°,可得AB∥AF,即可判定四边形ABDF是平行四边形,所以DF=AB=BC,故②正确.③由△ABE≌△ACF可得BE=CF,S△ABE=S△AFC,在△BCE和△FDC中,BC=DF,CE=CD,BE=CF ,可判定△BCE≌△FDC,所以S△BCE=S△FDC,即可得S△ABC=S△ABE+S△BCE=S△ACF+S△BCE=S△ABC=S△ACF+S△DCF,故③正确.④由△BCE≌△FDC,可得∠DBE=∠EFG,再由∠BED=∠FEG可判定△BDE∽△FGE,所以![]() =
=![]() ,即
,即![]() =
=![]() ,又因BD=2DC,DC=DE,可得
,又因BD=2DC,DC=DE,可得![]() =2,即FG=2EG.故④正确.
=2,即FG=2EG.故④正确.
考点:三角形综合题.
【题型】填空题
【结束】
19
【题目】先化简,再求值:(a+1-![]() )÷(
)÷(![]() ),其中a=2+
),其中a=2+![]() .
.
参考答案:
【答案】3+2![]()
【解析】分析:用分式的混合运算法则把原分式化简,再把a的值代入求解.
详解:(a+1-![]() )÷(
)÷(![]() )
)
=(![]() -
-![]() )÷(
)÷(![]() )
)
=![]() ·
·![]()
=a(a-2).
当a=2+![]() 时,
时,
原式=(2+![]() )(2+
)(2+![]() -2)
-2)
=3+![]() .
.
-
科目: 来源: 题型:
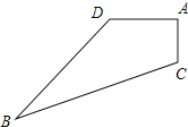
查看答案和解析>>【题目】已知某实验中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草坪,经测量∠A=90°,AC=3m,BD=12m,CB=13m,DA=4m,若每平方米草坪需要300元,间学校需要投入多少资金买草坪?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:

①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
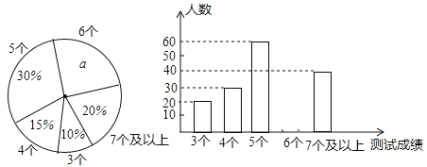
请你根据图中的信息,解答下列问题:
(1)补全条形图;
(2)直接写出在这次抽测中,测试成绩的众数和中位数;
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=15,AB=9.
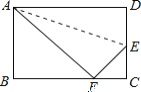
求:(1)FC的长;(2)EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由大小相同(棱长为1分米)的小立方块搭成的几何体如下图.


(1)请在右图的方格中画出该几何体的俯视图和左视图;
(2)图中有 块小正方体,它的表面积(含下底面)为 ;
(3)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要_______个小立方块,最多要_______个小立方块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=9,BC=6,AD为BC边上的高,过点A作AE//BC,过点D作DE//AC,AE与DE交于点E,AB与DE交于点F,连结BE.
求证:(1)四边形AEBD是矩形;(2)求四边形AEBD的周长.
相关试题

