【题目】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
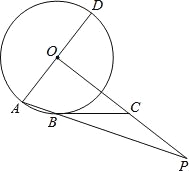
(1)求证:直线BC是⊙O的切线;
(2)若OA=3,AB=2,求BP的长.
参考答案:
【答案】(1)证明见解析(2)7
【解析】
试题分析:(1)连结OB.由等腰三角形的性质得到∠A=∠OBA,∠P=∠CBP,由于OP⊥AD,得到∠A+∠P=90°,于是得到∠OBA+∠CBP=90°,求得∠OBC=90°结论可得;
(2)连结DB.由AD是⊙O的直径,得到∠ABD=90°,推出Rt△ABD∽Rt△AOP,得到比例式![]() ,即可得到结果.
,即可得到结果.
试题解析:(1)连结OB.
∵OA=OB,∴∠A=∠OBA,
又∵BC=PC,
∴∠P=∠CBP,
∵OP⊥AD,
∴∠A+∠P=90°,
∴∠OBA+∠CBP=90°,
∴∠OBC=180°﹣(∠OBA+∠CBP)=90°,
∵点B在⊙O上,
∴直线BC是⊙O的切线,
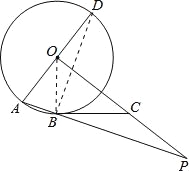
(2)如图,连结DB.
∵AD是⊙O的直径,
∴∠ABD=90°,
∴Rt△ABD∽Rt△AOP,
∴![]() ,即
,即![]() ,AP=9,
,AP=9,
∴BP=AP﹣BA=9﹣2=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(﹣3,4)关于原点对称的点的坐标是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,如果添加一个条件,就可推出ABCD是矩形,那么添加的条件可以是( )
A.AB=BC
B.AC=BD
C.AC⊥BD
D.AB⊥BD -
科目: 来源: 题型:
查看答案和解析>>【题目】已知ab=-3,a+b = 5,则10+a2b+ab2=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过14吨(含14吨)时,每吨按政府补贴优惠价收费;每月超过14吨时,超过部分每吨按市场调节价收费.小英家1月份用水20吨,交水费29元;2月份用水18吨,交水费24元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少?
(2)设每月用水量为
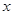 吨,应交水费为y元,写出y与
吨,应交水费为y元,写出y与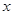 之间的函数关系式;
之间的函数关系式;(3)小英家3月份用水24吨,她家应交水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( )
A. x(x﹣1)=1035 B. x(x﹣1)=1035×2
C. x(x+1)=1035 D. 2x(x+1)=1035
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(2x-1)2-x(4x-1)
相关试题

