【题目】因式分解:m2﹣4n2=_____.
参考答案:
【答案】(m+2n)(m﹣2n)
【解析】m2﹣4n2,
=m2﹣(2n)2,
=(m+2n)(m﹣2n).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列性质中,菱形具有而平行四边形不具有的性质是( )
A. 对边平行且相等 B. 对角线互相平分
C. 对角线互相垂直 D. 对角互补
-
科目: 来源: 题型:
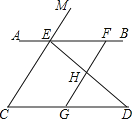
查看答案和解析>>【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程:x2﹣25=0的解是( )
A.x=5
B.x=﹣5
C.x1=﹣5,x2=5
D.x=±25 -
科目: 来源: 题型:
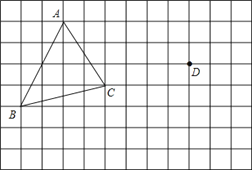
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并求△DEF的面积=
(2)若连接AD、CF,则这两条线段之间的关系是_________________;
(3)请在AB上找一点P,使得线段CP平分△ABC的面积,在图上作出线段CP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2010,最少经过几次操作 ( )
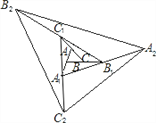
A. 6 B. 5 C. 4 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:
(1)4m2-9n2
(2)x2y-2xy2+y3
相关试题

