【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.
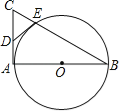
(1)若D为AC的中点,证明DE是⊙O的切线;
(2)若OA=![]() ,CE=1,求△ABC的面积.
,CE=1,求△ABC的面积.
参考答案:
【答案】(1)见解析;(2)2![]()
【解析】试题分析:(1)连接AE,OE,∠AEB=90°,∠BAC=90°,在Rt△ACE中,D为AC的中点,则DE=AD=CD=![]() AC,得出∠DEA=∠DAE,由OA=OE,得出∠OAE=∠OEA,则∠DEO=∠DEA+∠OEA=∠DAE+∠OAE=∠BAC=90°,即可得出结论;
AC,得出∠DEA=∠DAE,由OA=OE,得出∠OAE=∠OEA,则∠DEO=∠DEA+∠OEA=∠DAE+∠OAE=∠BAC=90°,即可得出结论;
(2)AB=2AO=2![]() ,由△BCA∽△BAE,得出
,由△BCA∽△BAE,得出![]() =
=![]() ,求出BE=3,BC=4,由勾股定理得AC=
,求出BE=3,BC=4,由勾股定理得AC=![]() =2,则S△ABC=
=2,则S△ABC=![]() ABAC代入即可得出结果.
ABAC代入即可得出结果.
(1)证明:连接AE,OE,如图所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵AC是⊙O的切线,
∴∠BAC=90°,
∵在Rt△ACE中,D为AC的中点,
∴DE=AD=CD=![]() AC,
AC,
∴∠DEA=∠DAE,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠DEO=∠DEA+∠OEA=∠DAE+∠OAE=∠BAC=90°,
∴OE⊥DE,
∵OE为半径,
∴DE是⊙O的切线;
(2)解:∵AO=![]() ,
,
∴AB=2AO=2![]() ,
,
∵∠CAB=∠AEB=90°,∠B=∠B,
∴△BCA∽△BAE,
∴![]() =
=![]() ,即AB2=BEBC=BE(BE+EC),
,即AB2=BEBC=BE(BE+EC),
∴(2![]() )2=BE2+BE,
)2=BE2+BE,
解得:BE=3或BE=﹣4(不合题意,舍去),
∴BE=3,
∴BC=BE+CE=3+1=4,
∴在Rt△ABC中,AC=![]() =
=![]() =2,
=2,
∴S△ABC=![]() ABAC=
ABAC=![]() ×2
×2![]() ×2=2
×2=2![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中有3个大小相同的小球,球面上分别写有数字1,2,3,从袋中随机摸出一个小球,记录下数字后放回,再随机摸出一个小球.
(1)请用树状图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出球上的数字的积为奇数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=4,动点P以每秒一个单位的速度从点A出发,沿对角线AC向点C移动,同时动点Q以相同的速度从点C出发,沿边CB向点B移动.设P,Q两点移动时间为t秒(0≤t≤4).
(1)用含t的代数式表示线段PC的长是 ;
(2)当△PCQ为等腰三角形时,求t的值;
(3)以BQ为直径的圆交PQ于点M,当M为PQ的中点时,求t的值.
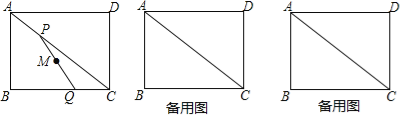
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程kx2+2x﹣1=0有两个不相等的实数根,则k的取值范围是( )
A.k>﹣1
B.k<﹣1
C.k≥﹣1且k≠0
D.k>﹣1且k≠0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,该抛物线顶点为D,对称轴交x轴于点H.
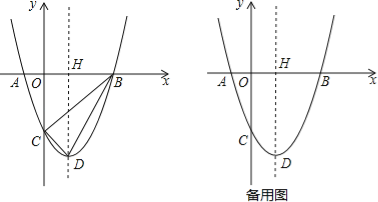
(1)求A,B两点的坐标;
(2)设点P在x轴下方的抛物线上,当∠ABP=∠CDB时,求出点P的坐标;
(3)以OB为边最第四象限内作等边△OBM.设点E为x轴的正半轴上一动点(OE>OH),连接ME,把线段ME绕点M顺时针旋转60°得MF,求线段DF的长的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x与双曲线y=
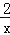 在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )
在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )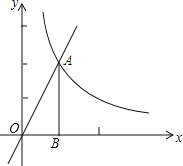
A.(2,0) B.(2,﹣1) C.(﹣2,1) D.(﹣1,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,该抛物线顶点为D,对称轴交x轴于点H.
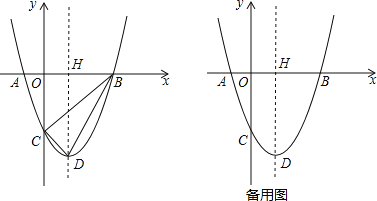
(1)求A,B两点的坐标;
(2)设点P在x轴下方的抛物线上,当∠ABP=∠CDB时,求出点P的坐标;
(3)以OB为边最第四象限内作等边△OBM.设点E为x轴的正半轴上一动点(OE>OH),连接ME,把线段ME绕点M顺时针旋转60°得MF,求线段DF的长的最小值.
相关试题

