【题目】如图,在四边形ABCD中,∠1=∠2,∠3=∠4,且∠D+∠C=220°,求∠AOB的度数. 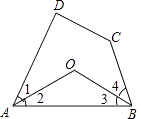
参考答案:
【答案】解:∵∠D+∠C+∠DAB+∠ABC=360°,∠D+∠C=220°,
∴∠DAB+∠ABC=360°﹣220°=140°,
∵∠1=∠2,∠3=∠4,
∴∠2+∠3=70°,
∴∠AOB=180°﹣70°=110°
【解析】首先根据四边形内角和为360度计算出∠DAB+∠ABC=360°﹣220°=140°,再根据∠1=∠2,∠3=∠4计算出∠2+∠3=70°,然后利用三角形内角和为180度计算出∠AOB的度数.
【考点精析】根据题目的已知条件,利用三角形的内角和外角和多边形内角与外角的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据共50个,分为6组,第一组的频数为5,第二组的频数为7,第三组的频数为8,第四组的频数为10,第五组的频率是0.2,则第六组的频数是( )
A. 10 B. 0.2 C. 40 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市电器销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段
销售量
销售收入
A型号
B型号
第一周
3台
5台
1800元
第二周
4台
10台
3100元
(1)求A、B两种型号的电风扇的销售价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能请给出采购方案.若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.
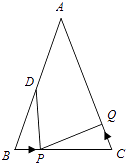
(1)如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过后,点P与点Q第一次在△ABC的边上相遇?(在横线上直接写出答案,不必书写解题过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】有一种记分方法:以90分为基准,95分记为+5分,某同学得87分,则应记为( )
A. +3分B. ﹣3分C. +7分D. ﹣7分
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)8+(﹣10)+(﹣2)﹣(﹣5)
(2 )﹣7+13﹣6+20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:﹣2(x2﹣3y)﹣[x2﹣3(2x2﹣3y)],其中x和y满足(x+1)2+|y+2|=0.
相关试题

