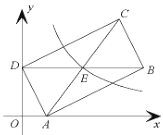
【题目】如图，在平面直角坐标系中，矩形的顶点，分别在轴、轴上，对角线轴，反比例函数的图象经过矩形对角线的交点，若点，，则的值为__________．

【答案】20

【解析】

根据平行于x轴的直线上任意两点纵坐标相同，可设B（x，4）．利用矩形的性质得出E为BD中点，∠DAB=90°．根据线段中点坐标公式得出E（x，4）．由勾股定理得出AD2+AB2=BD2，列出方程22+42+（x-2）2+42=x2，求出x，得到E点坐标，代入y=，利用待定系数法求出k．

∵BD∥x轴，D（0，4），
∴B、D两点纵坐标相同，都为4，
∴可设B（x，4）．
∵矩形ABCD的对角线的交点为E，
∴E为BD中点，∠DAB=90°．
∴E（x，4）．
∵∠DAB=90°，
∴AD2+AB2=BD2，
∵A（2，0），D（0，4），B（x，4），
∴22+42+（x-2）2+42=x2，
解得x=10，
∴E（5，4）．
∵反比例函数y=（k＞0，x＞0）的图象经过点E，
∴k=5×4=20．
故答案为20．

关闭