Question

【题目】如图，已知矩形ABCD（AB＜AD）．

（1）请用直尺和圆规按下列步骤作图，保留作图痕迹；
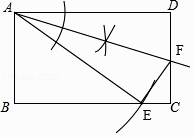
①以点A为圆心，以AD的长为半径画弧交边BC于点E，连接AE；
②作∠DAE的平分线交CD于点F；
③连接EF；
（2）在（1）作出的图形中，若AB=8，AD=10，则tan∠FEC的值为 ．

Answer 1

【答案】
（1）

解：如图所示；

（2）
【解析】解：（1.）如图所示；

（2.）由（1）知AE=AD=10、∠DAF=∠EAF，
∵AB=8，
∴BE= =6，
在△DAF和△EAF中，
∵ ，
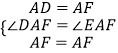∴△DAF≌△EAF（SAS），
∴∠D=∠AEF=90°，
∴∠BEA+∠FEC=90°，
又∵∠BEA+∠BAE=90°，
∴∠FEC=∠BAE，
∴tan∠FEC=tan∠BAE= = = ，
所以答案是： ．
【考点精析】解答此题的关键在于理解矩形的性质的相关知识，掌握矩形的四个角都是直角，矩形的对角线相等，以及对解直角三角形的理解，了解解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．