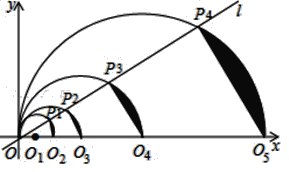
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=![]() x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和
x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和![]() 围成的弓形面积记为S1,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围
围成的弓形面积记为S1,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围![]() 成的弓形面积记为S2,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和
成的弓形面积记为S2,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和![]() 围成的弓形面积记为S3;…按此做法进行下去,其中S2018的面积为__________.
围成的弓形面积记为S3;…按此做法进行下去,其中S2018的面积为__________.
参考答案:
【答案】![]()
【解析】
连接P1O1,根据直线的函数解析式与特殊角的三角函数值得到∠P1OO1=30°,则∠P1O1O2=60°,再根据扇形面积公式与等边三角形的面积公式求得S1,S2,S3,S4找到规律,然后求解S2018即可.
解:如图,连接P1O1,
∵直线l的函数表达式为y=![]() x,
x,
∴tan P1OO1=![]() ,
,
∴∠P1OO1=30°,
∴∠P1O1O2=60°,
则S1=![]() ﹣
﹣![]() =
=![]() ,
,
同理可得S2=![]() ,
,
S3=![]() ,
,
S4=![]() =
=![]() ,
,
······
Sn=![]() ,
,
则当n=2018时,
S2018=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,直线
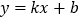 分别交x,y轴于点A(-8,0),B(0,6),C(m,0)是射线AO上一动点,⊙P过B,O,C三点,交直线AB于点D(B,D不重合).
分别交x,y轴于点A(-8,0),B(0,6),C(m,0)是射线AO上一动点,⊙P过B,O,C三点,交直线AB于点D(B,D不重合).(1)求直线AB的函数表达式.
(2)若点D在第一象限,且tan∠ODC=
 ,求点D的坐标.
,求点D的坐标.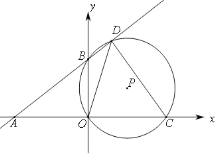
-
科目: 来源: 题型:
查看答案和解析>>【题目】某条公共汽车线路收支差额
 与乘客量
与乘客量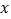 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额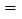 车票收入
车票收入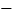 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )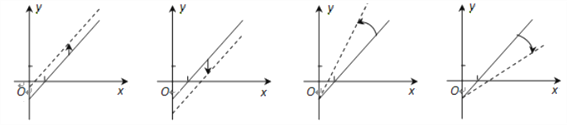
④ ③ ② ①
A. ①反映了建议(Ⅰ),③反映了建议(Ⅱ) B. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) D. ②反映了建议(Ⅱ),④反映了建议(Ⅰ)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B在双曲线y=
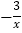 (x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=
(x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=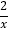 (x>0)上,此时□OABC的面积为__________.
(x>0)上,此时□OABC的面积为__________.
-
科目: 来源: 题型:
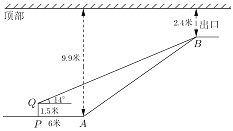
查看答案和解析>>【题目】地铁10号线某站点出口横截面平面图如图所示,电梯
 的两端分别距顶部9.9米和2.4米,在距电梯起点
的两端分别距顶部9.9米和2.4米,在距电梯起点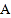 端6米的
端6米的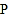 处,用1.5米的测角仪测得电梯终端
处,用1.5米的测角仪测得电梯终端 处的仰角为14°,求电梯
处的仰角为14°,求电梯 的坡度与长度.(参考数据:
的坡度与长度.(参考数据: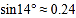 ,
,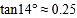 ,
,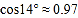 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的一条弦,点O在线段AC上,AC=AB,OC=3,sinA=
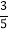 .求:(1)圆O的半径长;(2)BC的长.
.求:(1)圆O的半径长;(2)BC的长.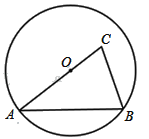
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是数值转换机的示意图,图②是小亮按照其对应关系画出的y与x的函数图象.已知点A的坐标为(0,3),点B的横坐标为4.
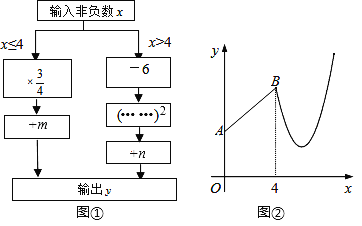
(1)求m、n的值.
(2)求输出y的最小值.
(3)当y=4时,求x的值.
相关试题

