【题目】如图1,抛物线y=﹣x2+bx+c与x轴交于A(2,0),B(﹣4,0)两点.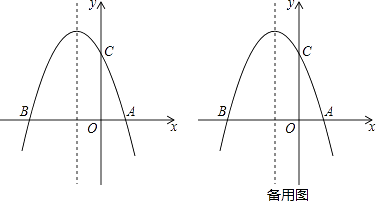
(1)求该抛物线的解析式;
(2)若抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在抛物线的第二象限图象上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若不存,请说明理由.
参考答案:
【答案】
(1)
解:将A(2,0),B(﹣4,0)代入得:
![]() ,
,
解得: ![]() ,
,
则该抛物线的解析式为:y=﹣x2﹣2x+8
(2)
解:如图1,点A关于抛物线对称轴的对称点为点B,设直线BC的解析式为:
y=kx+d,
将点B(﹣4,0)、C(0,8)代入得:
![]() ,
,
解得: ![]() ,
,
故直线BC解析式为:y=2x+8,
直线BC与抛物线对称轴 x=﹣1的交点为Q,此时△QAC的周长最小.
解方程组 ![]() 得,
得, ![]()
则点Q(﹣1,6)即为所求

(3)
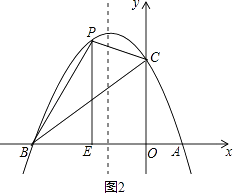
解:如图2,过点P作PE⊥x轴于点E,
P点(x,﹣x2﹣2x+8)(﹣4<x<0)
∵S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO﹣16
若S四边形BPCO有最大值,则S△BPC就最大
∴S四边形BPCO=S△BPE+S直角梯形PEOC
= ![]() BEPE+
BEPE+ ![]() OE(PE+OC)
OE(PE+OC)
= ![]() (x+4)(﹣x2﹣2x+8)+
(x+4)(﹣x2﹣2x+8)+ ![]() (﹣x)(﹣x2﹣2x+8+8)
(﹣x)(﹣x2﹣2x+8+8)
=﹣2(x+2)2+24,
当x=﹣2时,S四边形BPCO最大值=24,
∴S△BPC最大=24﹣16=8,
当x=﹣2时,﹣x2﹣2x+8=8,
∴点P的坐标为(﹣2,8).
【解析】(1)直接利用待定系数求出二次函数解析式即可;(2)首先求出直线BC的解析式,再利用轴对称求最短路线的方法得出答案;(3)根据S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO﹣16,得出函数最值,进而求出P点坐标即可.
-
科目: 来源: 题型:
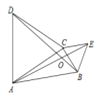
查看答案和解析>>【题目】如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O,则∠AOB的度数为________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地.
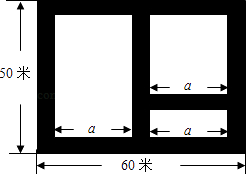
(1)设通道的宽度为x米,则a=(用含x的代数式表示);
(2)若塑胶运动场地总占地面积为2430平方米.请问通道的宽度为多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=BC=2,D为BC的中点,在AC边上存在一点E,连结ED,EB,则△BDE周长的最小值为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线
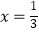 .则下列结论中,正确的是( )
.则下列结论中,正确的是( ) 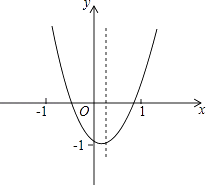
A.a<0
B.c<﹣1
C.a﹣b+c<0
D.2a+3b=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,若长方形的长BC为8,宽AB为4,求折叠后重叠部分的面积.
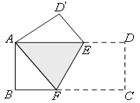
-
科目: 来源: 题型:
查看答案和解析>>【题目】图中,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,AB=2,半圆O的半径为2,则BC的长为( )
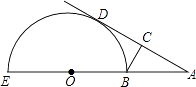
A.2
B.1
C.1.5
D.0.5
相关试题

