【题目】2015年3月3日到3月15日,两会在京矩形,雾霾防治问题受到国民的普遍关注,某报社决定以“对于雾霾,你最关注的话题是什么”为主题,通过街头随访和网络调查两种方式进行调查,根据调查所得数据绘制了表格.
最关注的话题 | 街头随访/人 | 网络调查/人 | 合计/人 |
雾霾是什么 | 120 | 200 | |
雾霾治理 | 40%a | 60%a | a |
雾霾中自我防护策略 | 600 | ||
其他话题 | 60 |
(1)参加本次街头随访和网络调查的总人数是多少人,a的值为多少;
(2)请你将以上表格中空白处补充完整;
(3)若在接受街头随访的人员中随机抽出一人,则抽到最关注“雾霾中自我防护策略”人员的概率是 多少? ;
参考答案:
【答案】解:(1)参加本次街头随访和网络调查的总人数是 2000人,a的值为 300;
(2)请你将以上表格中空白处补充完整;
街头随访/人 | 网络调查/人 | 合计/人 | |
雾霾是什么 | 80 | 120 | 200 |
雾霾治理 | 40%a | 60%a | a |
雾霾中自我防护策略 | 800 | 600 | 1400 |
其他话题 | 40 | 60 | 100 |
(3)若在接受街头随访的人员中随机抽出一人,则抽到最关注“雾霾中自我防护策略”人员的概率是 ![]() ;
;
【解析】(1)根据关注雾霾是什么的人数除以关注雾霾是什么所占的比例,可得调查总人数,根据调查总人数乘以雾霾治理所占的百分比,可得答案;
(2)根据调查总人数乘以雾霾自我防护策略所占的百分比,可得相应的人数,根据有理数的减法,可得其他话题人数,可得答案;
(3)根据街头随访中“雾霾自我防护策略的人数”除以街头随访的人数,可得答案;
【考点精析】本题主要考查了扇形统计图的相关知识点,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:



因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为
 和
和 (其中
(其中 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由. (3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y=a(x﹣1)2+c与x轴交于点A(
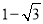 ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级5班的小明在解答此题时顿生灵感:过点P′作x轴的平行线交抛物线于C、D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比
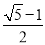 (约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:
(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据: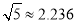 ,
,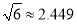 ,结果可保留根号)
,结果可保留根号)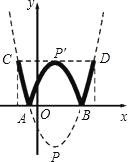
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(2,-3)关于x轴的对称点是( )
A. (-2,3) B. (2,3) C. (-2,-3) D. (2,-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2010年上海世博会即将举行,据有关方面统计,到时总共参与人数将达到4640万人次,其中4640万用科学记数法可表示为( )
A.0.464×109
B.4.64×108
C.4.64×107
D.46.4×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x(x-4)=2x-8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】冬季我国某城市某日最高气温为3℃,最低温度为﹣13℃,则该市这天的温差是( )
A. 13℃B. 14℃C. 15℃D. 16℃
相关试题

