【题目】如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM. 
(1)求证:EF= ![]() AC.
AC.
(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.
参考答案:
【答案】
(1)证明:∵CD=CB,点E为BD的中点,
∴CE⊥BD,
∵点F为AC的中点,
∴EF= ![]() AC
AC
(2)解:∵∠BAC=45°,CE⊥BD,
∴△AEC是等腰直角三角形,
∵点F为AC的中点,
∴EF垂直平分AC,
∴AM=CM,
∵CD=CM+DM=AM+DM,CD=CB,
∴BC=AM+DM
【解析】(1)根据等腰三角形三线合一的性质可得CE⊥BD,再根据直角三角形斜边上的中线等于斜边的一半可得EF= ![]() AC;(2)判断出△AEC是等腰直角三角形,根据等腰直角三角形的性质可得EF垂直平分AC,再根据线段垂直平分线上的点到两端点的距离相等可得AM=CM,然后求出CD=AM+DM,再等量代换即可得解.
AC;(2)判断出△AEC是等腰直角三角形,根据等腰直角三角形的性质可得EF垂直平分AC,再根据线段垂直平分线上的点到两端点的距离相等可得AM=CM,然后求出CD=AM+DM,再等量代换即可得解.
【考点精析】关于本题考查的等腰直角三角形和直角三角形斜边上的中线,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形斜边上的中线等于斜边的一半才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为
 的中点,BE⊥CD垂足为E.
的中点,BE⊥CD垂足为E.
(1)求∠BCE的度数;
(2)求证:D为CE的中点;
(3)连接OE交BC于点F,若AB=
 ,求OE的长度.
,求OE的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】成都某学校团委为了解本校七年级500各学生的平均每晚的睡眠时间,随机选择了该年级100名学生进行调查.关于下列说法:
①本次调查方式属于抽样调查
②每个学生是个体
③100名学生是总体的一个样本
④总体是该校七年级500名学生的平均每晚的睡眠时间
共中正确的说法有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距20 km,甲、乙两人都从A地去B地,如图,l1和l2分别表示甲、乙两人所走路程s(km)与时间t(h)之间的关系,下列说法:①乙晚出发1 h;②乙出发3 h后追上甲;③甲的速度是4 km/h;④乙先到达B地.其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】小英、爸爸、妈妈同时从家中出发到达同一目的地后都立即返回,小英去时骑自行车,返回时步行;妈妈去时步行,返回时骑自行车;爸爸往返都步行,三人步行的速度不等,小英与妈妈骑车的速度相等,每个人的行走路程与时间的关系分别是下图中的一个,走完一个往返,小英用时____________,爸爸用时____________,妈妈用时____________.
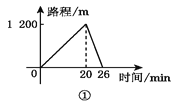
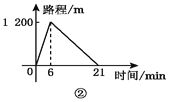
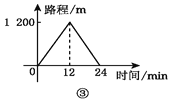
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,将△ECF绕点C逆时针旋转α角(0°<α<90°),得到△MCN,连接AM,BN.

(1)求证:AM=BN;
(2)当MA∥CN时,试求旋转角α的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图表示某市2016年6月份某一天的气温随时间变化的情况,请观察此图回答下列问题:
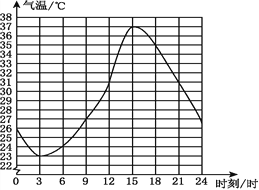
(1)这天的最高气温是多少摄氏度?
(2)这天共有多少个小时的气温在31 ℃以上?
(3)这天什么时间范围内气温在上升?
(4)请你预测一下,次日凌晨1时的气温大约是多少摄氏度?
相关试题

