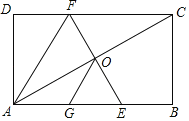
【题目】如图,在矩形ABCD中,O为AC中点,EF过点O且EF⊥AC分别交DC于点F,交AB于点E,点G是AE中点且∠AOG=30°,给出以下结论:
①∠AFC=120°;
②△AEF是等边三角形;
③AC=3OG;
④S△AOG=![]() S△ABC
S△ABC
其中正确的是______.(把所有正确结论的序号都选上)
参考答案:
【答案】①②④.
【解析】试题分析:根据直角三角形斜边上的中线等于斜边的一半可得OG=AG=GE=![]() AE,再根据等边对等角可得∠OAG=30°,∠EOG=60°,从而根据矩形的性质得到∠ACF=30°,因此由线段垂直平分线的性质可得FC=AF,因此可根据等边对等角得到∠FAE=30°,根据三角形的内角和求得∠AFC=120°,故①正确;
AE,再根据等边对等角可得∠OAG=30°,∠EOG=60°,从而根据矩形的性质得到∠ACF=30°,因此由线段垂直平分线的性质可得FC=AF,因此可根据等边对等角得到∠FAE=30°,根据三角形的内角和求得∠AFC=120°,故①正确;
由∠AFC=120°,∠FCA=30°,可知∠AFE=60°,因此△AEF是等边三角形,故②正确;
连接CE,则根据三角形的中位线可知CE=2OG,由矩形的性质可得四边形AECF是菱形,且![]() ,由OE=OG,OA=
,由OE=OG,OA=![]() AC,可知
AC,可知![]() ,解得AC=
,解得AC=![]() OG,故③不正确;
OG,故③不正确;
令AE=2a,则OG=OE=a,AO=![]() a,AC=2
a,AC=2![]() a,由S△AOE=
a,由S△AOE=![]() ×a×
×a×![]() a=
a=![]() 2,S矩形ABCD=3a×
2,S矩形ABCD=3a×![]() a=3
a=3![]() a2 ,即S△AOG=
a2 ,即S△AOG=![]() S△ABC,故④正确.
S△ABC,故④正确.
故答案为:①②④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学在一次用频率估计概率的实验中统计了某一结果出现的频率给出的统计图如图所示,则符合这一结果的实验可能是( )
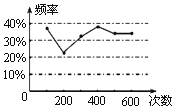
A.掷一枚正六面体的骰子,出现5点的概率
B.掷一枚硬币,出现正面朝上的概率
C.任意写出一个整数,能被2整除的概率
D.一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率 -
科目: 来源: 题型:
查看答案和解析>>【题目】若2m﹣4与3m﹣1是同一个数的平方根,则这个数是( )
A. 2 B. ﹣2 C. 4 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2016年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2018年投资7.2亿元人民币,那么每年投资的增长率为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件(1)打开电视机,正在播放新闻; (2)父亲的年龄比他儿子年龄大;(3)下个星期天会下雨;(4)抛掷两枚质地均匀的骰子,向上一面的点数之和是1;(5)一个实数的平方是正数(6)若a、b异号,则a+b<0.属于确定事件的有( )个.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图,则符合这一结果的实验可能是( )
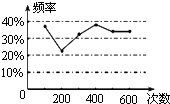
A.掷一枚正六面体的骰子,出现1点的概率
B.抛一枚硬币,出现正面的概率
C.从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
D.任意写一个整数,它能被2整除的概率 -
科目: 来源: 题型:
查看答案和解析>>【题目】3a(a2﹣2a+1)﹣2a2(a﹣3)= .
相关试题

