搜索
【题目】某校政教处倡导“光盘行动”，让同学们珍惜粮食，但发现还是有少数同学们就餐时剩余饭菜较多，为了让同学们理解这次活动的重要性，政教处在某天午餐中，分别按照七、八、九三个年级总人数的同样比例随机调查了三个年级部分同学这餐饭菜的剩余情况，分为三类：A（没有剩余）、B（有少量剩余）、C（剩余一半及以上），并将结果统计后绘制成了如图所示的不完整的统计图．
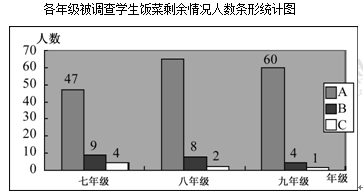
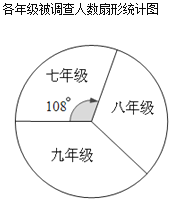
（1）这次被调查的同学共有名；
（2）八年级被调查的学生共有名；
（3）通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供8人用一餐．据此估算，该校1000名学生这餐饭菜没有浪费的学生有多少人？这餐浪费的食物可供多少人食用一餐？
参考答案：
【答案】（1）200；（2）75；（3）860； 40．
【解析】
试题分析：（1）（47+9+4）÷
=200（人）．
（2）200-60-（60+4+1）=75（人）．
（3）75-8-2=65，三个年级中被调查的学生没有浪费的比例为（47+65+60）÷200=
，
所以全校没有浪费学生数：1000×
=860（人），
可共食用一餐人数：1000×
=40（人）．
-
科目： 来源： 题型：
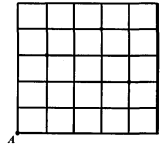
查看答案和解析>>【题目】如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负。如果从A到B记为：A→B（+1，+3）；从C到D记为：C→D（+1，－2）。其中第一个数表示左右方向，第二个数表示上下方向，那么图中
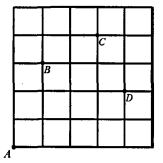
（1）A→C（ ， ），C→（-2， ）；
（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；
（3）假如这只甲虫从A处去甲虫P处的行走路线依次为
（＋2，＋2），（＋1，－1），（－2，＋3），请在图中标出P的位置．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一个口袋中装有4个只有颜色不同的球，其中3个白球，1个黑球．
（1）求从中随机抽取出一个黑球的概率是多少；
（2）若从口袋中摸出一个球，记下颜色后不放回，再摸出一个球。请列表或作出树状图，求两次都摸出白球的概率？
-
科目： 来源： 题型：
查看答案和解析>>【题目】九（1）班数学兴趣小组经过市场调查，整理出某种商品在第
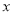（1≤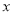≤90）天的售价与销量的相关信息如下表：时间x（天）
1≤x＜50
50≤x≤90
售价（元/件）
x+40
90
每天销量（件）
200﹣2x
已知该商品的进价为每件30元，设销售该商品的每天利润为
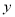元．（1）求出
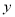与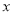的函数关系式；（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某果品批发公司以16元/千克购进一批樱桃．由往年市场销售情况的统计分析可知：当销售价定为25 元/千克时，每天可售出1 000 千克；若销售价定为20元/千克时，每天可售出2000千克．假设每天的销售量y（千克）与销售价x（元/千克）之间满足一次函数．
（1）试求y与x之间的函数关系式；
（2）在商品无积压且不考虑其他因素的条件下，销售价格定为多少时，才能使每天的销售毛利润W（元）最大？最大利润是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本小题满分9分）某百货大搂服装柜在销售中发现：“七彩”牌童装平均每天可售出20件，每件盈利40元．为了迎接“元旦”，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存．经市场调查发现：如果每件童装降价1元，那么平均每天就可多售出2件．
（1）要想平均每天销售这种童装盈利1200元，那么每件童装应降价多少元？
（2）用配方法说明：要想盈利最多，每件童装应降价多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
（1）20筐白菜中，最重的一筐比最轻的一筐多重多少千克？
（2）与标准重量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价2.6元，则出售这20筐白菜可卖多少元？（结果保留整数）
相关试题
