【题目】如图,已知AB∥CD,CN是∠BCE的平分线.
(1)若CM平分∠BCD,求∠MCN的度数;
(2)若CM在∠BCD的内部,且CM⊥CN于C,求证:CM平分∠BCD;
(3)在(2)的条件下,连结BM,BN,且BM⊥BN,∠MBN绕着B点旋转,∠BMC+∠BNC是否发生变化?若不变,求其值;若变化,求其变化范围.

参考答案:
【答案】(1)90°;(2)见解析;(3)∠BMC+∠BNC=180°不变,理由见解析
【解析】
(1)利用角平分线的定义和补角的定义可得结果;
(2)由垂直的定义可得∠MCN=90°,即∠BCN+∠BCM=90°,利用等式的性质可得2∠BCN+2∠BCM=180°,又因为∠BCE=2∠BCN,可得∠BCD=2∠BCM,即得结论;
(3)延长AB至F,过N,M分别作NG∥AB,MH∥AB,则有NG∥AB∥MH∥CD,利用平行线的性质易得∠BNG=∠ABN,∠CNG=∠ECN,∠BMH=∠FBM,∠CMH=∠DCM,由∠MBN=∠MCN=90°,可得∠ABN+∠FBM+∠ECN+∠DCM=180°,由角平分线的定义可得结论.
(1)∵CN,CM分别平分∠BCE和∠BCD,
∴BCN=![]() ∠BCE,∠BCM=
∠BCE,∠BCM=![]() ∠BCD,
∠BCD,
∵∠BCE+∠BCD=180°,
∴∠MCN=∠BCN+∠BCM=![]() ∠BCE+
∠BCE+![]() ∠BCD=
∠BCD=![]() (∠BCE+∠BCD)=90°;
(∠BCE+∠BCD)=90°;
(2)∵CM⊥CN,∴∠MCN=90°,即∠BCN+∠BCM=90°,
∴2∠BCN+2∠BCM=180°,
∵CN是∠BCE的平分线,∴∠BCE=2∠BCN,
∴∠BCE+2∠BCM=180°,
又∵∠BCE+∠BCD=180°,∴∠BCD=2∠BCM,
又∵CM在∠BCD的内部,∴CM平分∠BCD;
(3)如图,∠BMC+∠BNC=180°,延长AB至F,过N,M分别作NG∥AB,MH∥AB,则有NG∥AB∥MH∥CD,
∴∠BNG=∠ABN,∠CNG=∠ECN,∠BMH=∠FBM,∠CMH=∠DCM,
∵BM⊥BN,CM⊥CN,∴∠MBN=∠MCN=90°,
∵∠ABN+∠MBN+FBM=180°,∠ECN+∠MCN+∠DCM=180°,
∴∠ABN+∠FBM+∠ECN+∠DCM=180°,
∴∠BMC+∠BNC=∠BMH+∠CMH+∠BNG+∠CNG=∠ABN+∠FBM+∠ECN+∠DCM=180°,
∴∠BMC+∠BNC=180°不变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上一点,OC平分∠AOB,在直线AB另一侧,以O为顶点作∠DOE=90°.
(1)若∠AOE=48°,则∠BOD=______,∠AOE与∠BOD的关系是_______;
(2)∠AOE与∠COD有什么关系?请写出你的结论,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为( )
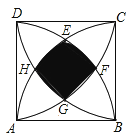
A.
B.
C.π
D.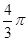
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=13,BC边上的高AD=12,则BC的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习有理数的乘法后,老师给同学们这样一道题目:计算:49
 ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下: 小明:原式=﹣
 ×5=﹣
×5=﹣ =﹣249
=﹣249 ;
; 小军:原式=(49+
 )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+ ×(﹣5)=﹣249
×(﹣5)=﹣249 ;
; (1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19
 ×(﹣8)
×(﹣8) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿CA往A运动,当运动到点A时停止.若设点D的运动时间为t秒,点D运动的速度为每秒2个单位长度.
(1)当t=2时,求CD、AD的长;
(2)在D运动过程中,△CBD能否为直角三角形,若不能,请说明理由,若能,请求出t的值;
(3)当t为何值时,△CBD是等腰三角形,请直接写出t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,a+b=80,ab<0.
(1)求出a,b的值;
(2)现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.
①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少?
②经过多长时间两只电子蚂蚁在数轴上相距20个单位长度?

相关试题

