【题目】如图,分别位于反比例函数y= ![]() ,y=
,y= ![]() 在第一象限图象上的两点A、B,与原点O在同一直线上,且
在第一象限图象上的两点A、B,与原点O在同一直线上,且 ![]() =
= ![]() .
. 
(1)求反比例函数y= ![]() 的表达式;
的表达式;
(2)过点A作x轴的平行线交y= ![]() 的图象于点C,连接BC,求△ABC的面积.
的图象于点C,连接BC,求△ABC的面积.
参考答案:
【答案】
(1)解:作AE、BF分别垂直于x轴,垂足为E、F.
∵△AOE∽△BOF,又 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
由点A在函数y= ![]() 的图象上,
的图象上,
设A的坐标是(m, ![]() ),
),
∴ ![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,
,
∴OF=3m,BF= ![]() ,即B的坐标是(3m,
,即B的坐标是(3m, ![]() ).
).
又点B在y= ![]() 的图象上,
的图象上,
∴ ![]() =
= ![]() ,
,
解得k=9,
则反比例函数y= ![]() 的表达式是y=
的表达式是y= ![]()

(2)解:由(1)可知,A(m, ![]() ),B(3m,
),B(3m, ![]() ),
),
又已知过A作x轴的平行线交y= ![]() 的图象于点C.
的图象于点C.
∴C的纵坐标是 ![]() ,
,
把y= ![]() 代入y=
代入y= ![]() 得x=9m,
得x=9m,
∴C的坐标是(9m, ![]() ),
),
∴AC=9m﹣m=8m.
∴S△ABC= ![]() ×8m×
×8m× ![]() =8.
=8.
【解析】(1)作AE、BF分别垂直于x轴,垂足为E、F,根据△AOE∽△BOF,则设A的横坐标是m,则可利用m表示出A和B的坐标,利用待定系数法求得k的值;(2)根据AC∥x轴,则可利用m表示出C的坐标,利用三角形的面积公式求解.
【考点精析】利用比例系数k的几何意义对题目进行判断即可得到答案,需要熟知几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了绿化环境,育英中学八年级三班同学都积极参加植树活动,今年植树节时,该班同学植树情况的部分数据如图所示,请根据统计图信息,回答下列问题:

(1)八年级三班共有多少名同学?
(2)条形统计图中,m= , n= .
(3)扇形统计图中,试计算植树2棵的人数所对应的扇形圆心角的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】耸立在临清市城北大运河东岸的舍利宝塔,是“运河四大名塔”之一(如图1).数学兴趣小组的小亮同学在塔上观景点P处,利用测角仪测得运河两岸上的A,B两点的俯角分别为17.9°,22°,并测得塔底点C到点B的距离为142米(A、B、C在同一直线上,如图2),求运河两岸上的A、B两点的距离(精确到1米).
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin17.9°≈0.31,cos17.9°≈0.95,tan17.9°≈0.32)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在推进城乡义务教育均衡发展工作中,我市某区政府通过公开招标的方式为辖区内全部乡镇中学采购了某型号的学生用电脑和教师用笔记本电脑,其中,A乡镇中学更新学生用电脑110台和教师用笔记本电脑32台,共花费30.5万元;B乡镇中学更新学生电脑55台和教师用笔记本电脑24台,共花费17.65万元.
(1)求该型号的学生用电脑和教师用笔记本电脑单价分别是多少万元?
(2)经统计,全部乡镇中学需要购进的教师用笔记本电脑台数比购进的学生用电脑台数的 少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.

(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+2x+c与y轴交于点A(0,6),与x轴交于点B(6,0),点P是线段AB上方抛物线上的一个动点.
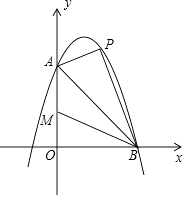
(1)求这条抛物线的表达式及其顶点坐标;
(2)当点P移动到抛物线的什么位置时,使得∠PAB=75°,求出此时点P的坐标;
(3)当点P从A点出发沿线段AB上方的抛物线向终点B移动,在移动中,点P的横坐标以每秒1个单位长度的速度变动,与此同时点M以每秒1个单位长度的速度沿AO向终点O移动,点P,M移动到各自终点时停止,当两个移点移动t秒时,求四边形PAMB的面积S关于t的函数表达式,并求t为何值时,S有最大值,最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
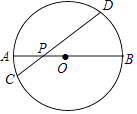
A.
B.2
C.2
D.8
相关试题

