【题目】在图1至图3中，点B是线段AC的中点，点D是线段CE的中点。四边形BCGF和CDHN都是正方形。AE的中点是M，FH的中点是P。
（1）如图1，点A、C、E在同一条直线上，根据图形填空：
①△BMF是__________三角形；
②MP与FH的位置关系是___________；MP与FH的数量关系是____________；
（2）将图1中的CE绕点C顺时针旋转一个锐角，得到图2，解答下列问题：
①证明：△BMF是等腰三角形；
②（1）中得到的MP与FH的位置关系和数量关系是否仍然成立？证明你的结论；
（3）将图2中的CE缩短到图3的情况，（2）中的三个结论还成立吗？（成立的不需要说明理由，不成立的需要说明理由）
【答案】 等腰直角 MP⊥FH MP=
FH
【解析】整体分析：
（1）①②由正方形的性质直接得到结论；（2）连接MH、MD，设FM与AC交于点Q，证明△FBM≌△MDH，判断△FMH是等腰直角三角形；（3）由（2）的证明可直接到得结论.
解：（1）①等腰直角；②MP⊥FH，MP=
FH；
（2）①∵B、D、M分别是AC、CE、AE的中点，
∴MB∥CD，且MB=CD=BC = BF，
∴△BMF是等腰三角形；
②仍然成立．证明如下：
如图，连接MH、MD，设FM与AC交于点Q．
由①可知MB∥CD，MB=CD，
∴四边形BCDM是平行四边形，
∴∠CBM=∠CDM．
又∵∠FBQ=∠HDC，∴∠FBM=∠MDH，
∴△FBM≌△MDH，∴FM=MH，∠MFB=∠HMD，
∴∠FMH=∠FMD－∠HMD=∠AQM－∠MFB=∠FBC=90°，
∴△FMH是等腰直角三角形．
∵P是FH的中点，∴MP⊥FH，MP=
FH；
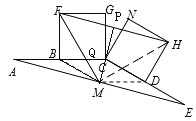
（3）△BMF不是等腰三角形，理由如下：
∵MB=CD，CD≠BC，∴MB≠BF，且∠FBM＞90°；
MP⊥FH仍然成立，MP=
FH仍然成立．
科目：初中数学 来源： 题型：
【题目】在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处，观察到飞艇底部标志P处的仰角为45°，又观其在湖中之像的俯角为60°，则飞艇底部P距离湖面的高度为（参考等式： 
= 
）（ ）
A.25 
+75
B.50 +50
C.75 +75
D.50 +100
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予以证明．（写出一种即可）
关系：①AD∥BC，②AB=CD，③∠A=∠C，④∠B+∠C=180°．
已知：在四边形ABCD中， ， ；
求证：四边形ABCD是平行四边形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小红星期天从家里出发汽车去舅舅家做客，当她骑了一段路时，想起要买个礼物送给表弟，于是又折回到刚经过的一家商店，买好礼物后又继续骑车去舅舅家，以下是她本次去舅舅家所用的时间与路程的关系式示意图．根据图中提供的信息回答下列问题：
（1）小红家到学校的路程是______米，小红在商店停留了______分钟；
（2）在整个去舅舅家的途中哪个时间段小红骑车速度最快?最快速度是多少米/分？
（3）本次去舅舅家的行程中，小红一共行驶了多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将一张矩形纸板按图中虚线裁剪成九块，其中有两块是边长都为
的大正方形，两块是边长都为
的小正方形，五块是长为
、宽为
的全等小矩形，且
> 
．（以上长度单位：cm）
（1）观察图形，可以发现代数式
可以因式分解为 ；
（2）若每块小矩形的面积为10
，四个正方形的面积和为58
，试求图中所有裁剪线（虚线部分）长之和．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线AB，CD相交于点O，OA平分∠EOC．
（1）若∠EOC=80°，求∠BOD的度数；
（2）若∠EOC=∠EOD，求∠BOD的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“五一”期间，某商铺经营某种旅游纪念品．该商铺第一次批发购进该纪念品共花费3 000元，很快全部售完．接着，该商铺第二次批发购进该纪念品共花费9000元．已知第二次所购进该纪念品的数量是第一次的2倍还多300个，第二次的进价比第一次的进价提高了20%．
（1）求第一次购进该纪念品的进价是多少元？
（2）若该纪念品的两次售价均为9元/个，两次所购纪念品全部售完后，求该商铺两次共盈利多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】企业举行“爱心一日捐”活动，捐款金额分为五个档次，分别是50元，100元，150元，200元，300元．宣传小组随机抽取部分捐款职工并统计了他们的捐款金额，绘制成两个不完整的统计图，请结合图表中的信息解答下列问题：
（1）宣传小组抽取的捐款人数为_____人，请补全条形统计图；
（2）在扇形统计图中，求100元所对应扇形的圆心角的度数；
（3）已知该企业共有500人参与本次捐款，请你估计捐款总额大约为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，∠B=30°，BC=12． 
（1）用尺规作图的方法作AB的垂直平分线MN，分别交BC、AB于点M、N（保留作图痕迹，不要求写作法）；
（2）求第（1）题中的CM的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com