搜索
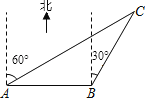
【题目】在一自助夏令营活动中，小明同学从营地A出发，要到A地的北偏东60°方向的C处，他先沿正东方向走了200m到达B地，再沿北偏东30°方向走，恰能到达目的地C（如图），那么，由此可知，B、C两地相距 m．
参考答案：
【答案】200
【解析】
试题分析：首先把实际问题转化为直角三角形问题来解决，由已知可推出∠ABC=90°+30°=120°，∠BAC=90°﹣60°=30°，再由三角形内角和定理得∠ACB=30°，从而求出B、C两地的距离．
解：由已知得：
∠ABC=90°+30°=120°，
∠BAC=90°﹣60°=30°，
∴∠ACB=180°﹣∠ABC﹣∠BAC=180°﹣120°﹣30°=30°，
∴∠ACB=∠BAC，
∴BC=AB=200．
故答案为：200．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如(x＋m)与(x＋3)的乘积中不含x的一次项，则m的值为( )．
A. －3 B. 3 C. 0 D. 1
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了参加中考体育测试，甲、乙、丙三位同学进行足球传球训练，球从一个人脚下随机传到另一个人脚下，且每位传球人传给其余两人的机会是均等的，由甲开始传球，共传球三次．
（1）请利用树状图列举出三次传球的所有可能情况；
（2）求三次传球后，球回到甲脚下的概率；
（3）三次传球后，球回到甲脚下的概率大还是传到乙脚下的概率大？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣
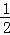x2+bx+c交x轴于点A，B，交y轴于点C，点A的坐标是（﹣1，0），点C的坐标是（0，2）．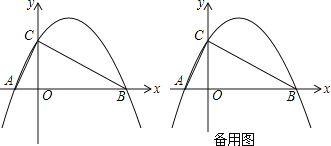
（1）求该抛物线的解析式；
（2）已知点P是抛物线的上的一个动点，点N在x轴上．
①若点P在x轴上方，且△APN是等腰直角三角形，求点N的坐标；
②若点P在x轴下方，且△ANP与△BOC相似，请直接写出点N的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】能够将一个三角形的面积平分的线段是( )
A. 一边上的高线 B. 一个内角的角平分线 C. 一边上的中线 D. 一边上的中垂线
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AC∥BD，连接AB，直线AC、BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连接PA，PB，构成∠PAC，∠APB，∠PBD三个角．（提示：有公共端点的两条重合的射线所组成的角是0°角）
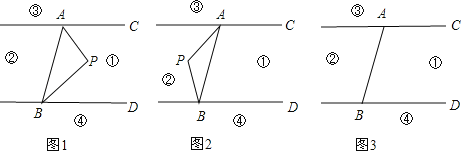
（1）当动点P落在第①部分时，求证：∠APB=∠PAC+∠PBD；
（2）当动点P落在第②部分时，∠APB=∠PAC+∠PBD是否成立？（直接回答成立或不成立）
（3）当动点P落在第③部分时，全面探究∠PAC，∠APB，∠PBD之间的关系，并写出动点P的具体位置和相应的结论．选择其中一种结论加以证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列长度的三条线段不可能组成三角形的是（ ）
A. 1、2、3 B. 2、3、4 C. 3、4、5 D. 4、5、6
相关试题
