【题目】如图,已知线段AB=a,点C在直线AB上,![]() .
.
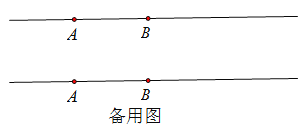
(1)用尺规作图画出点C;
(2)若点P在线段BC上,且BP:PC=2:3,D为线段PC的中点,求BD的长(用含a的代数式表示);
(3)在(2)的条件下,若AD=3cm,求a的值.
参考答案:
【答案】(1)详见解析;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)分两种情况画图:点C在线段AB的延长线上或C点在线段AB的反向延长线上;
(2)对于图1,BC=2a,由BP:PC=2:3可计算出BP=![]() BC=
BC=![]() a,PC=
a,PC=![]() BC=
BC=![]() a,再由D为线段PC的中点得到PD=
a,再由D为线段PC的中点得到PD=![]() PC=
PC=![]() a,然后利用BD=BP+PD计算得BD=
a,然后利用BD=BP+PD计算得BD=![]() a;对于图2,BC=4a,由BP:PC=2:3可计算得BP=
a;对于图2,BC=4a,由BP:PC=2:3可计算得BP=![]() BC=
BC=![]() a,PC=
a,PC=![]() BC=
BC=![]() a,再由D为线段PC的中点得到PD=
a,再由D为线段PC的中点得到PD=![]() PC=
PC=![]() a,然后利用BD=BP+PD计算可得BD=
a,然后利用BD=BP+PD计算可得BD=![]() a;(3)对于图1,先得到CD=PD=
a;(3)对于图1,先得到CD=PD=![]() a,再计算出AD=AC-CD=
a,再计算出AD=AC-CD=![]() a,则
a,则![]() a=3,然后解方程即可;对于图2,先得到CD=PD=
a=3,然后解方程即可;对于图2,先得到CD=PD=![]() a,利用计算出AD=BC-CD=
a,利用计算出AD=BC-CD=![]() a,则
a,则![]() a=3,然后解方程即可.
a=3,然后解方程即可.
试题解析::解:(1)如图所示:当点C在线段AB的延长线上,如图1:
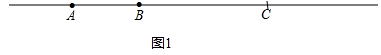
当C点在线段AB的反向延长线上时,如图2:
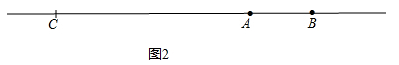 ;
;
(2)对于图1,
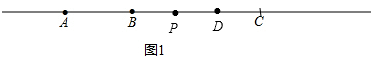
∵AB=a,∴AC=3a,∴BC=2a,
∵BP:PC=2:3,∴BP=![]() BC=
BC=![]() 2a=
2a=![]() a,PC=
a,PC=![]() BC=
BC=![]() a,
a,
∵D为线段PC的中点,∴PD=![]() PC=
PC=![]() a,
a,
∴BD=BP+PD=![]() a+
a+![]() a=
a=![]() a;
a;
对于图2,

BC=AB+AC=4a,
∵BP:PC=2:3,∴BP=![]() BC=
BC=![]() 4a=
4a=![]() a,PC=
a,PC=![]() BC=
BC=![]() a,
a,
∵D为线段PC的中点,∴PD=![]() PC=
PC=![]() a,∴BD=BP+PD=
a,∴BD=BP+PD=![]() a+
a+![]() a=
a=![]() a;
a;
(3)对于图1,CD=PD=![]() a,AD=AC-CD=3a-
a,AD=AC-CD=3a-![]() a=
a=![]() a=3,解得a=
a=3,解得a=![]() (cm);
(cm);
对于图2,CD=PD=![]() a,AD=BC-CD=4a-
a,AD=BC-CD=4a-![]() a=
a=![]() a=3,解得a=
a=3,解得a=![]() (cm).
(cm).
考点:分类讨论;线段的计算;一元一次方程的应用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据报道,2016年单位就业人员年平均工资超过70300元,将数70300用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任何整数m,多项式(4m+5)2-9一定能( )
A. 被8整除 B. 被m整除
C. 被m-91整除 D. 被2m-1整除
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( )
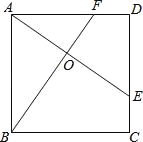
A.4个 B.3个 C.2个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O的半径为5cm,两条弦AB∥CD,AB=8cm、CD=6cm,则两条弦之间的距离为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b-2)2=0

(1)求线段AB的长;
(2)如图1 点C在数轴上对应的数为x,且x是方程2x+1=
 x-5的根,在数轴上是否存在点P使PA+PB=
x-5的根,在数轴上是否存在点P使PA+PB= BC+AB?若存在,求出点P对应的数;若不存在,说明理由;
BC+AB?若存在,求出点P对应的数;若不存在,说明理由;(3)如图2,若P点是B点右侧一点,PA的中点为M,N为PB的三等分点且靠近于P点,当P在B的右侧运动时,有两个结论:①PM-
 BN的值不变;②
BN的值不变;② PM+
PM+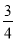 BN的值不变,其中只有一个结论正确,请判断正确的结论,并求出其值
BN的值不变,其中只有一个结论正确,请判断正确的结论,并求出其值 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(x,y)在第四象限,且|x|=3,|y|=5,则点P的坐标是______。
相关试题

