搜索
【题目】为响应金华市政府发出的创文明城市号召，学校总务处刘老师用M元购买花卉发给各班美化卫生保洁区.若以2棵树和3株花为一份，则可以买60份；若以2棵树和6株花为一份，则可以买40份.设树的单价为x元/棵，花的单价为y元/株.
(1)当
时，求树和花的单价.
(2)若用这M元全部购买花，总共可以买几株花?
参考答案：
【答案】(1)树的单价为9元/棵，花的单价为6元/株；(2)总共可以买360株.
【解析】
（1）本题中的相等关系是“以2棵树和3株花为一份，则可以买60份”和“以2棵树和6株花为一份，则可以买40份”，列方程组求解即可．
（2）由（1）可得树和花的单价比，可计算出全部购买花，总共可以买多少株花．
(1)由题意得
，
解得：
．
答：树的单价为9元/棵，花的单价为6元/株．
(2)∵树和花的单价比为
，以2棵树和3株花为一份，可以买60份，
∴ 若用这笔钱全部购买花，总共可以买
(株) ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，△ABC的位置如图所示（每个小方格都是边长为1个单位长度的正方形）．
（1）将△ABC沿x轴方向向左平移6个单位，画出平移后得到的△A1B1C1；
（2）将△ABC绕着点A顺时针旋转90°，画出旋转后得到的△AB2C2，并直接写出点B2、C2的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列各图，（1）第①个图中有1个三角形，第②个图中有3个三角形，第③个图中有6个三角形，第④个图中有 个三角形，第10个图中有 个三角形……，根据这个规律可知第n个图中有 个三角形（用含正整数n的式子表示）．
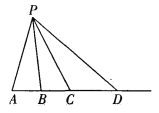
(2)问在上述图形中是否存在这样的一个图形，该图形中共有35个三角形？若存在，求出n的值；若不存在请说明理由．
(3)在图中，点B是线段AC的中点，D为AC延长线上的一个动点，记△PDA的面积为S1，△PDB的面积为S2，△PDC的面积为S3．请直接写出S1.S2.S3之间的数量关系：
-
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数填入对应的横线内：
－38，4.8，+84，3.1416，0，2008，－
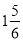，－0.142，95%，+
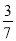．非负整数：______________________________________________________________
负整数：______________________________________________________________
正分数：_____________________________________________________________
负有理数：______________________________________________________________
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于二次函数
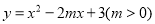，有下列说法:①如果
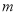=2，则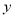
有最小值－1; ②如果当
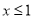时
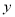随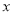
的增大而减小，则
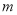=1;③如果将它的图象向左平移3个单位后的函数的最小值是－9，则
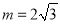;④如果当
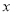=1时的函数值与
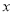=2015时的函数值相等，则当
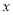=2016时的函数值为3.其中正确的说法是_____________.(把你认为正确的结论的序号都填上) -
科目： 来源： 题型：
查看答案和解析>>【题目】图1，抛物线与x轴交于A（﹣1，0），B（3，0），顶点为D（1，﹣4），点P为y轴上一动点．
（1）求抛物线的解析式；
（2）在y轴的负半轴上是否存在点P，使△BDP是等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．
（3）如图2，点
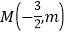在抛物线上，求
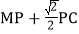的最小值．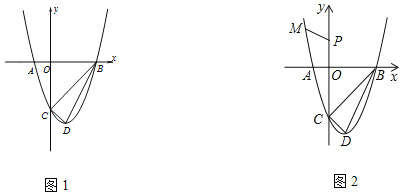
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知在平面直角坐标系中有 A(-2，1)， B(3， 1)，C(2， 3)三点，请回答下列问题:
(1)在坐标系内描出点A， B， C的位置.
(2)画出
关于直线x=-1对称的
，并写出各点坐标.(3)在y轴上是否存在点P，使以A，B， P三点为顶点的三角形的面积为10?若存在，请直接写出点P的坐标:若不存在，请说明理由.
相关试题
