【题目】如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于 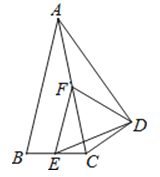
参考答案:
【答案】![]()
【解析】解:∵E、F分别是BC、AC的中点,∠CAD=∠CAB=26°,
∴EF是△ABC的中位线,
∴EF=![]() AB,∠EFC=∠CAB=26°.
AB,∠EFC=∠CAB=26°.
∵AB=AC,△ACD是直角三角形,点E是斜边AC的中点,
∴DF=AF=CF,
∴DF=EF,∠CAD=∠ADF=26°.
∵∠DFC是△AFD的外角,
∴∠DFC=26°+26°=52°,
∴∠EFD=∠EFC+∠DFC=26°+52°=78°,
∴∠EDF=![]() =51°.
=51°.
故答案为:![]() .
.
先根据题意判断出△DEF的形状,由平行线的性质得出∠EFC的度数,再由三角形外角的性质求出∠DFC的度数,再根据三角形内角和定理即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正数的两个平方根分别为a和2a-9.
(1)求a的值,并求这个正数;
(2)求17-9a2的立方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】人在灯光下走动,当人远离灯光时,其影子的长度将( )
A.逐渐变短
B.逐渐变长
C.不变
D.以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(-1,2),B(3,2),C(1,-2).
(1)求证:AB∥x轴;
(2)求△ABC的面积;
(3)若在y轴上有一点P,使S△ABP=
 S△ABC,求点P的坐标.
S△ABC,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
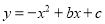 经过
经过 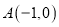 ,
, 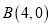 两点,与
两点,与 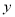 轴相交于点
轴相交于点 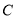 ,连接
,连接  .点
.点  为抛物线上一动点,过点
为抛物线上一动点,过点  作
作  轴的垂线
轴的垂线  ,交直线
,交直线 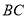 于点
于点 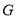 ,交
,交  轴于点
轴于点  .
.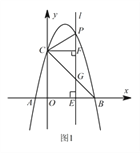
Ⅰ 求抛物线的表达式;
Ⅱ 当
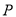 位于
位于  轴右边的抛物线上运动时,过点
轴右边的抛物线上运动时,过点  作
作  直线
直线  ,
,  为垂足.当点
为垂足.当点 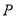 运动到何处时,以
运动到何处时,以 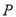 ,
, 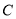 ,
,  为顶点的三角形与
为顶点的三角形与 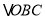 相似?并求出此时点
相似?并求出此时点  的坐标;
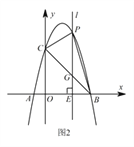
的坐标;Ⅲ 如图2,当点
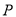 在位于直线
在位于直线 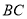 上方的抛物线上运动时,连接
上方的抛物线上运动时,连接 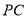 ,
,  .请问
.请问 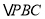 的面积
的面积 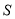 能否取得最大值?若能,请求出最大面积
能否取得最大值?若能,请求出最大面积 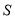 ,并求出此时点
,并求出此时点 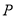 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三人拿出同样多的钱,合伙订购同种规格的若干件商品.商品买来后,甲、乙分别比丙多拿了12、9件商品,最后结算时,乙付给丙20元,那么,甲应付给丙元.
相关试题

