【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
参考答案:
【答案】(1)W1=-2x+60x+8000,W2=-19x+950;(2)当x=10时,W总最大为9160元.
【解析】
(1)第二期培植的盆景比第一期增加x盆,则第二期培植盆景(50+x)盆,花卉(50-x)盆,根据盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元,②花卉的平均每盆利润始终不变,即可得到利润W1,W2与x的关系式;
(2)由W总=W1+W2可得关于x的二次函数,利用二次函数的性质即可得.
(1)第二期培植的盆景比第一期增加x盆,则第二期培植盆景(50+x)盆,花卉[100-(50+x)]=(50-x)盆,由题意得
W1=(50+x)(160-2x)=-2x+60x+8000,
W2=19(50-x)=-19x+950;
(2)W总=W1+W2=-2x+60x+8000+(-19x+950)=-2x+41x+8950,
∵-2<0,![]() =10.25,
=10.25,
故当x=10时,W总最大,
W总最大=-2×10+41×10+8950=9160.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学完《平面直角坐标系》和《一次函数》这两章后,老师布置了这样一道思考题:已知:如图,在长方形
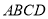 中,
中,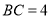 ,
,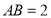 ,点
,点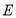 为
为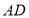 的中点,
的中点,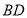 和
和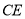 相交于点
相交于点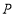 .求
.求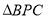 的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以
的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以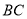 所在的直线为
所在的直线为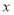 轴,以
轴,以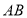 所在的直线为
所在的直线为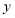 轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点
轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点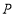 的坐标,从而求得
的坐标,从而求得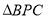 的面积.请你按照小明的思路解决这道思考题.
的面积.请你按照小明的思路解决这道思考题.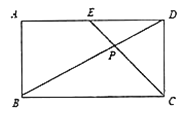
-
科目: 来源: 题型:
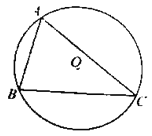
查看答案和解析>>【题目】如图,⊙O为锐角△ABC的外接圆,半径为5.
(1)用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦BC的距离为3,求弦CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图部分信息如下:
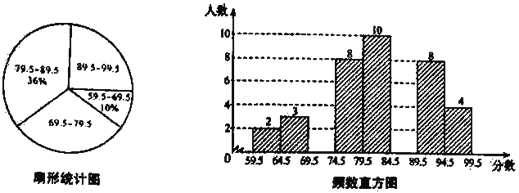
(1)本次比赛参赛选手共有 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 ;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,已知
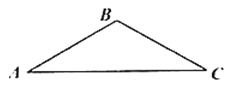
中,已知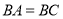 ,
,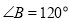 ,
,
(1)画
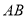 的垂直平分线
的垂直平分线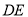 交
交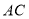 、
、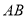 于点
于点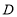 、
、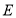 (保留作图痕迹,作图痕迹请加黑描重);
(保留作图痕迹,作图痕迹请加黑描重);(2)求
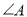 的度数;
的度数;(3)若
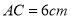 ,求
,求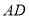 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】“中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)共抽取了多少个学生进行调查?
(2)将图甲中的折线统计图补充完整.
(3)求出图乙中B等级所占圆心角的度数.

-
科目: 来源: 题型:
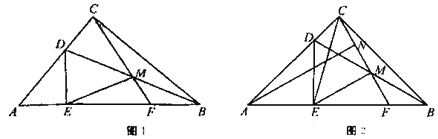
查看答案和解析>>【题目】如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点M为BD中点,CM的延长线交AB于点F.
(1)求证:CM=EM;
(2)若∠BAC=50°,求∠EMF的大小;
(3)如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM.
相关试题

