【题目】观察:① 1×3+1=22② 2×4+1=32③ 3×5+1=42 ④ 4×6+1=52
请你用含一个字母的等式表示你发现的规律:.
参考答案:
【答案】n(n+2)+1=(n+1)2
【解析】假设第一个数字为n,则第二个数字为(n+2),等号后面的数字为(n+1),然后根据给出的式子得出规律.
首先观察第一个等式的特点:左边变化的量:1与3相差2,右边变化的量:22,而2恰好是1与3中间的数,即 1×3+1=22;再观察其它的等式,可以发现也有此规律,根据此规律即可列出等式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的边数为6,则这个多边形的内角和为 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,下列各点在第二象限的是( )
A. (3,1) B. (3,-1)
C. (-3,1) D. (-3,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的括号里-2,100π,-5
 ,0.8,-|+5.2|,0,0.1010010001…,-(-4
,0.8,-|+5.2|,0,0.1010010001…,-(-4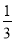 )
)正有理数集合:{ }
整数集合:{ }
负分数集合:{ }
无理数集合:{ }
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业今年1月份产值为x万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值是( )
A.(1﹣10%)(1+15%)x万元
B.(1﹣10%+15%)x万元
C.(x﹣10%)(x+15%)万元
D.(1+10%﹣15%)x万元 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx﹣3自变量x的部分取值和对应的函数值y如下表:
x
…
﹣2
﹣1
0
1
2
3
…
y
…
5
0
﹣3
﹣4
﹣3
0
…
则在实数范围内能使得y﹣5<0成立的x的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)写出绝对值不大于4的所有整数;
(2)求满足(1)中条件的所有整数的和.
相关试题

