【题目】如图,在平面直角坐标系中,点A和点B的坐标分别为A(4,0)、B(0,2),将△ABO绕点P(2,2)顺时针旋转得到△OCD,点A、B和O的对应点分别为点O、C和D,
(1)画出△OCD,并写出点C和点D的坐标;
(2)连接AC,在直线AC的右侧取点M,使∠AMC=45°,
①若点M在x轴上,则点M的坐标为 ;
②若△ACM为直角三角形,求点M的坐标;
(3)若点N满足∠ANC>45°,请确定点N的位置(不要求说明理由).

参考答案:
【答案】(1)画图详见解析;C(2,4),D(0,4);(2)①(6,0);②点M的坐标为(8,2)或(6,6);(3)点N在以点(5,3)或点(1,1)为圆心,以![]() 为半径的圆内.
为半径的圆内.
【解析】
试题分析:(1)先确定出OA,OB,再由旋转的性质得出OD=4,CD=2,即可得出结论;
(2)先构造出满足条件的点M的位置,利用等腰三角形的性质和等腰直角三角形的性质即可得出结论;
(3)同(2)①的方法得出结论.
试题解析:(1)如图1,
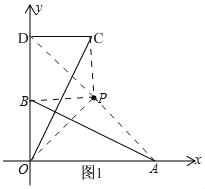
∵点A和点B的坐标分别为A(4,0)、B(0,2),
∴OA=4,OB=2,
由旋转知,△POD≌△PAO,△PCD≌△PBO,
∴OD=OA=4,CD=OB=2,
∴C(2,4),D(0,4);
(2)①如图2,
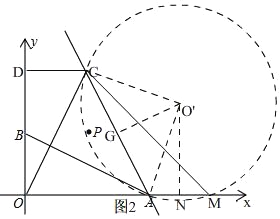
∵A(4,0),C(2,4),
∴AC=![]() ,
,
以AC为斜边在直线AC右侧作等腰直角三角形ACO′,以O′为圆心,O′A为半径作圆,
∴∠AMC=![]() ∠AO′C=45°,
∠AO′C=45°,
过点O′作O′G⊥AC,
∵A(4,0),C(2,4),
∴G(3,2),
∴直线AC的解析式为y=﹣2x+8,
∴直线O′G的解析式为y=![]() ,
,
设点O′的坐标为(m,![]() ),
),
∴![]() =
=![]() =
=![]() ,
,
∴m=5或m=1(点O′在直线AC右侧,所以舍去),
∴O′(5,3),
∴O′A=![]() ,
,
在Rt△AO′N中,O′N=3,AN=![]() =1,
=1,
∴AM=2AN=2,
∴M(6,0);
故答案为:(6,0),
②如图3,
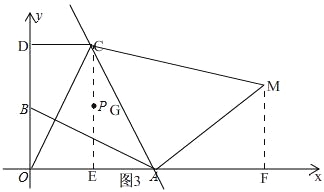
当∠CAM为直角时,
分别过点C,M作x轴的垂线,垂足分别为E,F.
∵CO=CA,
∴OE=AE=![]() OA=2,
OA=2,
∴∠CAE+∠ACE=90°,
∵∠CAE+∠FAM=90°,
∴∠ACE=∠FAM,
在△ACE和△MAF中∠AEC=∠MFA,∠ACE=∠FAM,AC=AM,
∴△CEA≌△AFM,
∴MF=AE=2,AF=CE=4,
∴OF=8,
∴M(8,2);
当∠ACM为直角时,
同理可得M(6,6);
综上所述,点M的坐标为(8,2)或(6,6).
(3)如图3,
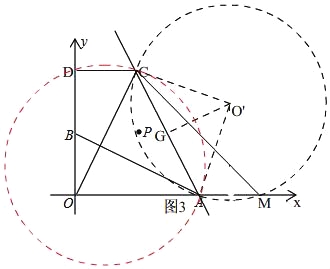
∵A(4,0),C(2,4),
∴AC=![]() ,
,
以AC为斜边在直线AC右侧作等腰直角三角形ACO′,以O′为圆心,O′A为半径作圆,
∴∠ANC<![]() ∠AO′C=45°,
∠AO′C=45°,
过点O′作O′G⊥AC,
∵A(4,0),C(2,4),
∴G(3,2),直线AC的解析式为y=﹣2x+8,
∴直线O′G的解析式为y=![]() ,
,
设点O′的坐标为(m,![]() ),
),
∴![]() =
=![]() =
=![]() ,
,
∴m=5或m=1,
∴O′(5,3)或(1,1),
∵A(4,0),
∴O′A=![]() ,
,
∴点N在以点(5,3)或点(1,1)为圆心,以![]() 为半径的圆内.
为半径的圆内.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=
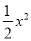 +mx﹣2m﹣2与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,
+mx﹣2m﹣2与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,(1)当m=1时,求点A和点B的坐标;
(2)抛物线上有一点D(﹣1,n),若△ACD的面积为5,求m的值;
(3)P为抛物线上A、B之间一点(不包括A、B),PM⊥x轴于点M,求
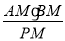 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式的计算,结果正确的是( )
A. 3x+2y= 5xy B. -y2-y2=0 C. 7x+7x=14x2 D. -y2x+x y2=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司制作毕业纪念册的收费如下:设计费与加工费共1000元,另外每册收取材料费4元,则总收费y与制作纪念册的册数x的函数关系式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)画出数轴,并用数轴上的点表示下列各数:﹣5,2.5,﹣ ,0,3
,0,3  ;
;
(2)用“<”号把各数从小到大连起来. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小华在一起玩数字游戏,他们每人取了一张数字卡片,拼成了一个两位数.小明说:“哇!这个两位数的十位数字与个位数字之和恰好是9.”他们又把这两张卡片对调,得到了一个新的两位数,小华说:“这个两位数恰好也比原来的两位数大9.”
那么,你能回答以下问题吗?
(1)他们取出的两张卡片上的数字分别是几?
(2)第一次,他们拼出的两位数是多少?
(3)第二次,他们拼成的两位数又是多少呢?请你好好动动脑筋哟!
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A. 经过两点有且只有一条直线
B. 为了解全国七年级学生的数学成绩,选用普查的方式比较合适
C. 绝对值最小的数是零
D. 折线统计图能清楚地反映事物的变化情况
相关试题

