13．如图，在∠AOB的边OA上过到点O的距离为1，3，5，7…的点作互相平行的直线，分别与OB相交，得到如图中所示的阴影梯形，它们的面积依次记为S1，S2，S3，…．则$\frac{{S}_{2014}}{{S}_{2013}}$=$\frac{4027}{4025}$．

分析 设△OCD的面积为1，根据相似三角形的面积比等于相似比的平方计算，总结规律，计算即可．

解答 解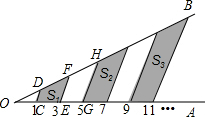：设△OCD的面积为1，
∵CD∥EF，
∴△OCD∽△OEF，又$\frac{OC}{OE}$=$\frac{1}{3}$，
∴△OEF的面积为9，
∴S1=8，
同理，S2=24，S3=40…，Sn=8（2n-1），
$\frac{{S}_{2014}}{{S}_{2013}}$=$\frac{8（2×2014-1）}{8（2×2013-1）}$=$\frac{4027}{4025}$，
故答案为：$\frac{4027}{4025}$．

点评 本题考查的是相似三角形的性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．

关闭