【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线y=﹣ ![]() x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式;
(2)若PE=5EF,求m的值;
(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:将点A、B坐标代入抛物线解析式,得:
![]() ,解得
,解得 ![]() ,
,
∴抛物线的解析式为:y=﹣x2+4x+5
(2)
解:∵点P的横坐标为m,
∴P(m,﹣m2+4m+5),E(m,﹣ ![]() m+3),F(m,0).
m+3),F(m,0).
∴PE=|yP﹣yE|=|(﹣m2+4m+5)﹣(﹣ ![]() m+3)|=|﹣m2+
m+3)|=|﹣m2+ ![]() m+2|,
m+2|,
EF=|yE﹣yF|=|(﹣ ![]() m+3)﹣0|=|﹣
m+3)﹣0|=|﹣ ![]() m+3|.
m+3|.
由题意,PE=5EF,即:|﹣m2+ ![]() m+2|=5|﹣
m+2|=5|﹣ ![]() m+3|=|
m+3|=| ![]() m+15|
m+15|
①若﹣m2+ ![]() m+2=
m+2= ![]() m+15,整理得:2m2﹣17m+26=0,
m+15,整理得:2m2﹣17m+26=0,
解得:m=2或m= ![]() ;
;
②若﹣m2+ ![]() m+2=﹣(
m+2=﹣( ![]() m+15),整理得:m2﹣m﹣17=0,
m+15),整理得:m2﹣m﹣17=0,
解得:m= ![]() 或m=
或m= ![]() .
.
由题意,m的取值范围为:﹣1<m<5,故m= ![]() 、m=
、m= ![]() 这两个解均舍去.
这两个解均舍去.
∴m=2或m= ![]()
(3)
解:方法一:假设存在.
作出示意图如下:

∵点E、E′关于直线PC对称,
∴∠1=∠2,CE=CE′,PE=PE′.
∵PE平行于y轴,∴∠1=∠3,
∴∠2=∠3,∴PE=CE,
∴PE=CE=PE′=CE′,即四边形PECE′是菱形.
当四边形PECE′是菱形存在时,
由直线CD解析式y=﹣ ![]() x+3,可得OD=4,OC=3,由勾股定理得CD=5.
x+3,可得OD=4,OC=3,由勾股定理得CD=5.
过点E作EM∥x轴,交y轴于点M,易得△CEM∽△CDO,
∴ ![]() ,即
,即 ![]() ,解得CE=
,解得CE= ![]() |m|,
|m|,
∴PE=CE= ![]() |m|,又由(2)可知:PE=|﹣m2+
|m|,又由(2)可知:PE=|﹣m2+ ![]() m+2|
m+2|
∴|﹣m2+ ![]() m+2|=
m+2|= ![]() |m|.
|m|.
①若﹣m2+ ![]() m+2=
m+2= ![]() m,整理得:2m2﹣7m﹣4=0,解得m=4或m=﹣
m,整理得:2m2﹣7m﹣4=0,解得m=4或m=﹣ ![]() ;
;
②若﹣m2+ ![]() m+2=﹣
m+2=﹣ ![]() m,整理得:m2﹣6m﹣2=0,解得m1=3+
m,整理得:m2﹣6m﹣2=0,解得m1=3+ ![]() ,m2=3﹣
,m2=3﹣ ![]() .
.
由题意,m的取值范围为:﹣1<m<5,故m=3+ ![]() 这个解舍去.
这个解舍去.
当四边形PECE′是菱形这一条件不存在时,
此时P点横坐标为0,E,C,E'三点重合与y轴上,也符合题意,
∴P(0,5)
综上所述,存在满足条件的点P,可求得点P坐标为(0,5),(﹣ ![]() ,
, ![]() ),(4,5),(3﹣
),(4,5),(3﹣ ![]() ,2
,2 ![]() ﹣3)
﹣3)
方法二:
若E(不与C重合时)关于直线PC的对称点E′在y轴上,则直线CD与直线CE′关于PC轴对称.
∴点D关于直线PC的对称点D′也在y轴上,
∴DD′⊥CP,∵y=﹣ ![]() x+3,
x+3,
∴D(4,0),CD=5,
∵OC=3,
∴OD′=8或OD′=2,
①当OD′=8时,D′(0,8),设P(t,﹣t2+4t+5),D(4,0),C(0,3),
∵PC⊥DD′,∴KPC×KDD′=﹣1,
∴ ![]() ,
,
∴2t2﹣7t﹣4=0,
∴t1=4,t2=﹣ ![]() ,
,
②当OD′=2时,D′(0,﹣2),
设P(t,﹣t2+4t+5),
∵PC⊥DD′,∴KPC×KDD′=﹣1,
∴ ![]() =﹣1,
=﹣1,
∴t1span>=3+ ![]() ,t2=3﹣
,t2=3﹣ ![]() ,
,
∵点P是x轴上方的抛物线上一动点,
∴﹣1<t<5,
∴点P的坐标为(﹣ ![]() ,
, ![]() ),(4,5),(3﹣
),(4,5),(3﹣ ![]() ,2
,2 ![]() ﹣3).
﹣3).
若点E与C重合时,P(0,5)也符合题意.
综上所述,存在满足条件的点P,可求得点P坐标为(0,5),(﹣ ![]() ,
, ![]() ),(4,5),(3﹣
),(4,5),(3﹣ ![]() ,2
,2 ![]() ﹣3)
﹣3)

【解析】(1)利用待定系数法求出抛物线的解析式;(2)用含m的代数式分别表示出PE、EF,然后列方程求解;(3)解题关键是识别出当四边形PECE′是菱形,然后根据PE=CE的条件,列出方程求解;当四边形PECE′是菱形不存在时,P点y轴上,即可得到点P坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱体铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上). 现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示.①图2中折线ABC表示___________槽中水的深度与注水时间之间的关系(选填“甲”或“乙”);②点B的纵坐标表示的实际意义是___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元. ①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】
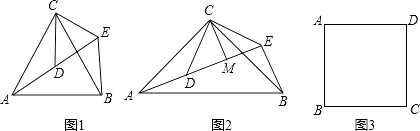
(1)问题发现 如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:
①∠AEB的度数为;
②线段AD,BE之间的数量关系为 .
(2)拓展探究 如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
(3)解决问题 如图3,在正方形ABCD中,CD=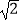 ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( )

A.AG=BG
B.AB∥EF
C.AD∥BC
D.∠ABC=∠ADC -
科目: 来源: 题型:
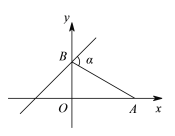
查看答案和解析>>【题目】如图,已知A点的坐标为
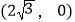 ,直线
,直线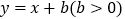 与y轴交于点B,连接AB,若
与y轴交于点B,连接AB,若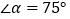 ,则
,则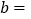 ____________.
____________. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,老师提出如下问题:如何使用尺规完成“过直线l外一点A作已知直线l的平行线”.

小云的作法如下:
(1)在直线l 上任取一点B,以点B为圆心,AB长为半径作弧, 交直线l 于点C;
(2)分别以A,C为圆心,以AB长为半径作弧,两弧相交于点D;
(3)作直线AD.
所以直线AD即为所求.
老师说:“小云的作法正确”.
请回答:小云的作图依据是____________.
相关试题

