【题目】如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1), 则△OCD与四边形ABDC的面积比为( )
A.1:2
B.1:3
C.1:4
D.1:8
参考答案:
【答案】D
【解析】解:设OA所在直线为y=kx, 将点A(6,3)代入得:3=6k,
解得:k= ![]() ,
,
∴OA所在直线解析式为y= ![]() x,
x,
当x=2时,y= ![]() ×2=1,
×2=1,
∴点C在线段OA上,
∵AB,CD都垂直于x轴,且CD=1、AB=3,
∴△OCD∽△OAB,
∴ ![]() =(
=( ![]() )2=
)2= ![]() ,
,
则△OCD与四边形ABDC的面积比为1:8,
故选:D.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,纸片□ABCD中,AD=5,S□ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
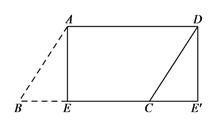
(2)如图,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.
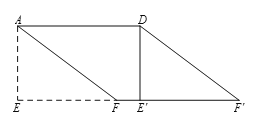
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育委员统计了全班学生“1分钟跳绳”的次数,绘制成如下两幅统计图:

根据这两幅统计图的信息完成下列问题
(1)这个班共有学生多少人?并补全频数分布直方图;
(2)如果将“1分钟跳绳”的次数大于或等于180个定为优秀,请你求出这个班“1分钟跳绳”的次数达到优秀的百分率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时: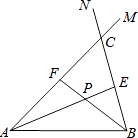
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32 ,求AQ的长.
,求AQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.

相关试题

