Question

【题目】如图1，在平面直角坐标系xOy中，点B（﹣2，2），过反比例函数y=（x＜0，常数k＜0）图象上一点A（﹣，m）作y轴的平行线交直线l：y=x+2于点C，且AC=AB．

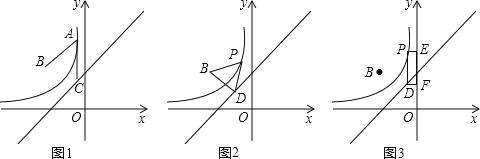
（1）分别求出m、k的值，并写出这个反比例函数解析式；

（2）发现：过函数y=（x＜0）图象上任意一点P，作y轴的平行线交直线l于点D，请直接写出你发现的PB，PD的数量关系 ；

应用：①如图2，连接BD，当△PBD是等边三角形时，求此时点P的坐标；

②如图3，分别过点P、D作y的垂线交y轴于点E、F，问是否存在点P，使得矩形PEFD的周长取得最小值？若存在，请求出此时点P的坐标及矩形PEFD的周长；若不存在，请说明理由．

Answer 1

【答案】（1）y=﹣（x＜0）（2）PB=PD①（1﹣， +1）；②存在，（﹣1，2），4

【解析】

试题分析：（1）求出AC、AB的表达式，根据AC=AB求出m的值，然后利用待定系数法求出k的值即可；

（2）设P（﹣m，）（m＞0），则D（﹣m，﹣m+2），根据勾股定理求出PB的长即可；①由△PBD是等边三角形，于是得到PB=BD=PD，根据等边三角形的性质得到（2﹣m）=（+m﹣2）解得：m=3﹣，或m=﹣1，于是得到P（﹣3，）或P（1﹣， +1）；②根据矩形的周长的计算公式得到矩形PEFD的周长=（﹣）2+4，根据二次函数的性质即可得到结论．

试题解析：（1）AC=m﹣，AB=，

∵AC=AF，

∴m=4，

∴点A（﹣，4），

∴k=﹣2，

∴y=﹣（x＜0）；

（2）设P（﹣m，）（m＞0），则D（m，m+2），

∴PD=﹣（﹣m+2）=+m﹣2，

BP==+m﹣2，

∴PD=PB；

故答案为：PB=PD；

①∵△PBD是等边三角形，

∴PB=BD=PD，

∵PD∥y轴，

∴（2﹣m）=（+m﹣2）

∴+m﹣2=，

∴m=3﹣，或m=﹣1，

∴P（1﹣， +1）；

②答：存在满足题设条件的点P．

设P（﹣m，）（m＞0），则D（﹣m，﹣m+2），

∴矩形PEFD的周长=2（PD+PE）=2（+m﹣2+m）=+4m﹣4=（﹣）2+4，

∴当﹣=0，即m=2时，P（﹣1，2）时，矩形PEFD的周长取得最小值为4．