【题目】如图①，在等腰中，如图①，在等腰中，，平分交于点.点为线段上一点（不与端点、重合），，与的延长线交于点，与交于点，连接、、．

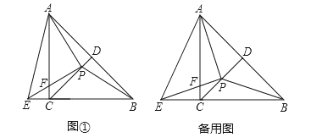
（1）求证：；

（2）求的度数；

（3）探究线段、之间的数量关系，并证明．

【答案】（1）证明见解析；（2）∠EAP=45°；（3）EC=PD．

【解析】

（1）根据等腰直角三角形的性质可得CD是AB的垂直平分线，根据垂直平分线的性质可得AP=BP；

（2）由∠ACE=∠APE=90°，可得点A，点P，点C，点E四点共圆，可得∠AEP=∠ACD=45°，即可求∠EAP的度数；

（3）过点E作EH⊥CD于点H，根据“AAS”可证△APD≌△PEH，可得EH=PD，根据勾股定理可求EC=EH，即可得EC=PD．

证明：（1）∵∠ACB=90°，AC=BC，CD平分∠ACB，

∴CD⊥AB，AD=BD，∠ACD=∠BCD=∠CAD=∠DBC=45°，

∴CD是AB的垂直平分线

∴AP=BP，

（2）∵∠ACE=∠APE=90°，

∴点A，点P，点C，点E四点共圆，

∴∠AEP=∠ACD=45°，且AP⊥EP，

∴∠EAP=45°

（3）EC=PD，理由如下：

如图，过点E作EH⊥CD于点H，

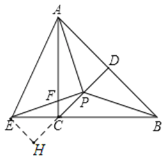
∵∠EAP=∠AEP=45°，

∴AP=PE，

∵∠APE=90°=∠ADP

∴∠APD+∠PAD=90°，∠APD+∠EPH=90°，

∴∠PAD=∠EPH，且AP=PE，∠EHP=∠ADP=90°

∴△APD≌△PEH（AAS）

∴EH=PD，

∵∠ECH=∠DCB=45°，EH⊥CD

∴∠HEC=∠HCE=45°

∴EH=CH

在Rt△ECH中

∴EC=PD．

关闭