【题目】关于x的方程为x2+(m+2)x+2m﹣1=0.
(1)证明:方程有两个不相等的实数根;
(2)是否存在实数m,使方程的两个实数根互为相反数?若存在,求出m的值;若不存在,请说明理由.
参考答案:
【答案】(1)方程有两个不相等的实数根;(2)存在, m=﹣2时,方程的两根互为相反数
【解析】试题分析:(1)运用一元二次方程根的判别式,当△>0,一元二次方程有两个不相等的实数根,要证明方程有两个不相等的实数根,即只要证出△>0即可.(2)要使方程的两个实数根互为相反数,利用根与系数的关系,得出x1+x2=![]() =0,代入求出m的值即可.
=0,代入求出m的值即可.
试题解析:
(1)∵关于x的方程为x2+(m+2)x+2m﹣1=0.
∴△=(m+2)2﹣4(2m﹣1)=m2+4m+4﹣8m+4=m2﹣4m+4+4=(m﹣2)2+4>0,
∴方程有两个不相等的实数根;
(2)存在,设方程的两根为x1,x2,
∵关于x的方程为x2+(m+2)x+2m﹣1=0.
∴根据根与系数的关系得,x1+x2=﹣(m+2),
∵方程的两个实数根互为相反数,
∴x1+x2=0,
即:﹣(m+2)=0,
∴m=﹣2.
即:m=﹣2时,方程的两根互为相反数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的右侧作正方形ADEF,连接CF.
(1)观察猜想:如图(1),当点D在线段BC上时,
①BC与CF的位置关系是: ;
②BC、CD、CF之间的数量关系为: (将结论直接写在横线上)
(2)数学思考:如图(2),当点D在线段CB的延长线上时,上述①、②中的结论是否仍然成立?若成立,请给予证明,若不成立,请你写出正确结论再给予证明.

-
科目: 来源: 题型:
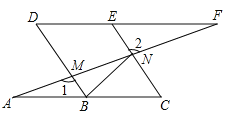
查看答案和解析>>【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上
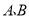 两点相距
两点相距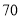 个单位长度,机器人从
个单位长度,机器人从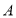 点出发去
点出发去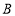 点,
点,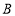 点在
点在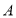 点右侧.规定向右为前进,第一次它前进
点右侧.规定向右为前进,第一次它前进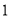 个单位长度,第二次它后退
个单位长度,第二次它后退 个单位长度,第三次再前进
个单位长度,第三次再前进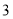 个单位长度,第四次又后退
个单位长度,第四次又后退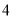 个单位长度……按此规律行进,如果
个单位长度……按此规律行进,如果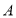 点在数轴上表示的数为
点在数轴上表示的数为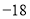 ,那么
,那么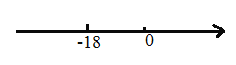
(1)求出
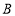 点在数轴上表示的数.
点在数轴上表示的数.(2)经过第七次行进后机器人到达点
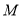 ,第八次行进后到达点
,第八次行进后到达点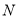 ,点
,点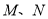 到
到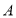 点的距离相等吗?请说明理由.
点的距离相等吗?请说明理由.(3)机器人在未到达
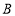 点之前,经过
点之前,经过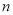 次(
次(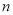 为正整数)行进后,它在数轴上表示的数应如何用含
为正整数)行进后,它在数轴上表示的数应如何用含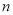 的代数式表示?
的代数式表示?(4)如果
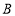 点在原点的右侧,那么机器人经过
点在原点的右侧,那么机器人经过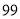 次行进后,它在
次行进后,它在 点的什么位置?请通过计算说明.
点的什么位置?请通过计算说明. -
科目: 来源: 题型:
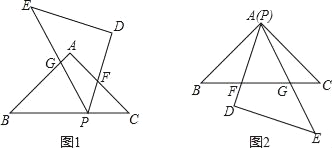
查看答案和解析>>【题目】如图,△ABC、△DEP是两个全等的等腰直角三角形,∠BAC=∠PDE=90°.
(1)若将△DEP的顶点P放在BC上(如图1),PD、PE分别与AC、AB相交于点F、G.求证:△PBG∽△FCP;
(2)若使△DEP的顶点P与顶点A重合(如图2),PD、PE与BC相交于点F、G.试问△PBG与△FCP还相似吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
相关试题

