【题目】为方便市民通行,某广场计划对坡角为30°,坡长为60米的斜坡AB进行改造,在斜坡中点D处挖去部分坡体(阴影表示),修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
(1)若修建的斜坡BE的坡角为36°,则平台DE的长约为多少米?
(2)在距离坡角A点27米远的G处是商场主楼,小明在D点测得主楼顶部H 的仰角为30°,那么主楼GH高约为多少米?(结果取整数,参考数据:sin36°=0.6,cos36°=0.8,tan36°=0.7, ![]() =1.7)
=1.7)
参考答案:
【答案】
(1)解:∵修建的斜坡BE的坡角(即∠BEF)为36°,
∴∠BEF=36°,
∵∠DAC=∠BDF=30°,AD=BD=30,
∴BF= ![]() BD=15,DF=15
BD=15,DF=15 ![]() ≈25.98,
≈25.98,
EF= ![]() =
= ![]() ≈21.43
≈21.43
故:DE=DF﹣EF=4(米);
(2)解:过点D作DP⊥AC,垂足为P. 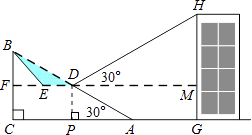
在Rt△DPA中,DP= ![]() AD=
AD= ![]() ×30=15,
×30=15,
PA=ADcos30°= ![]() ×30=15
×30=15 ![]() ,
,
在矩形DPGM中,MG=DP=15,DM=PG=15 ![]() +27,
+27,
在Rt△DMH中,
HM=DMtan30°= ![]() ×(15
×(15 ![]() +27)=15+9
+27)=15+9 ![]() ,
,
GH=HM+MG=15+15+9 ![]() ≈45米.
≈45米.
答:建筑物GH高约为45米.
【解析】(1)因为修建的斜坡BE的坡角(即∠BEF)为36°,由∠DAC=∠BDF,AD=BD,得到BF= ![]() BD,DF≈25.98,根据解直角三角形EF=
BD,DF≈25.98,根据解直角三角形EF= ![]() =
= ![]() ≈21.43;得到DE=DF﹣EF;(2)根据实际问题得到图形,在Rt△DPA中,DP=
≈21.43;得到DE=DF﹣EF;(2)根据实际问题得到图形,在Rt△DPA中,DP= ![]() AD,PA=ADcos30°,在矩形DPGM中,MG=DP,在Rt△DMH中,HM=DMtan30°,得到GH=HM+MG.
AD,PA=ADcos30°,在矩形DPGM中,MG=DP,在Rt△DMH中,HM=DMtan30°,得到GH=HM+MG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
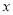 的不等式组
的不等式组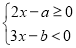 整数解为1、2,如果把适合这个不等式组的整数
整数解为1、2,如果把适合这个不等式组的整数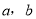 组成有序数对
组成有序数对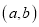 ,那么对应在平面直角坐标系上的点共有的个数为_______.
,那么对应在平面直角坐标系上的点共有的个数为_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(
 ,0),有下列结论:①abc>0;
,0),有下列结论:①abc>0;
②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0; ⑤a﹣b≥m(am﹣b);
其中所有正确的结论是( )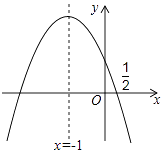
A.①②③
B.①③④
C.①②③⑤
D.①③⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,EG∥AD,找出图中的等腰三角形,并给出证明.
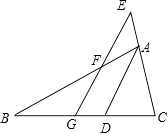
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+2
x+2  与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和
与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和  个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
(1)求点A,点B的坐标;
(2)用含t的代数式分别表示EF和AF的长;
(3)当四边形ADEF为菱形时,试判断△AFG与△AGB是否相似,并说明理由.
(4)是否存在t的值,使△AGF为直角三角形?若存在,求出这时抛物线的解析式;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )

A.
B.
C.
D.
相关试题

