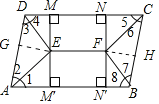
【题目】如图，在ABCD中，DC＞AD，四个角的平分线AE，DE，BF，CF的交点分别是E，F，过点E，F分别作DC与AB间的垂线MM'与NN'，在DC与AB上的垂足分别是M，N与M′，N′，连接EF．

（1）求证：四边形EFNM是矩形；

（2）已知：AE=4，DE=3，DC=9，求EF的长．

【答案】（1）证明见解析；（2）EF=4

【解析】（1）要说明四边形EFNM是矩形，有ME⊥CD，FN⊥CD条件，还缺ME=FN，过点E、F分别作AD、BC的垂线，垂足分别是G、H．利用角平分线上的点到角两边的距离相等可得结论；

（2）利用平行四边形的性质，证明直角△DEA，并求出AD的长．利用全等证明△GEA≌△CNF，△DME≌△DGE从而得到DM=DG，AG=CN，再利用线段的和差关系，求出MN的长得结论．

（1）如图，过点E、F分别作AD、BC的垂线，垂足分别是G、H，

∵∠3=∠4，∠1=∠2，EG⊥AD，EM⊥CD，EM′⊥AB，

∴EG=ME，EG=EM′，

∴EG=ME=ME′=MM′，

同理可证：FH=NF=N′F=NN′，

∵CD∥AB，MM′⊥CD，NN′⊥CD，

∴MM′=NN′，

∴ME=NF=EG=FH，

又∵MM′∥NN′，MM′⊥CD，

∴四边形EFNM是矩形；

（2）∵DC∥AB，

∴∠CDA+∠DAB=180°，

∵∠3=∠CDA ，∠2=∠DAB，

∴∠3+∠2=90°，

在Rt△DEA，∵AE=4，DE=3，

∴AB==5，

∵四边形ABCD是平行四边形，

∴∠DAB=∠DCB，

又∵∠2=∠DAB，∠5=∠DCB，

∴∠2=∠5，

由（1）知GE=NF，

在Rt△GEA和Rt△CNF中

，

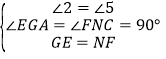∴△GEA≌△CNF，

∴AG=CN，

在Rt△DME和Rt△DGE中，

∵DE=DE，ME=EG，

∴△DME≌△DGE，

∴DG=DM，

∴DM+CN=DG+AG=AB=5，

∴MN=CD﹣DM﹣CN=9﹣5=4，

∵四边形EFNM是矩形，

∴EF=MN=4.

关闭