【题目】作等腰△ABC底边BC上的高线AD,按以下作图方法正确的个数有( )个.
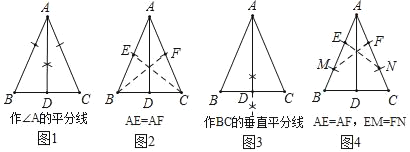
A. 1B. 2C. 3D. 4
参考答案:
【答案】D
【解析】
图3 ,AD垂直平分BC,故图3正确;图1,根据等腰三角形三线合一,故图1正确;图2,先证明△AEC≌△AFB,再证明AD垂直平分BC,故图2正确;图4先证明△AEN≌△AFM和EOM≌△FON,再证明△AOE≌△AOF,进而得到AD平分平分∠BAC,由三线合一可知图4正确.
解:图1,在等腰△ABC中,AD平分∠BAC,则AD⊥BC(三线合一),故图1正确.
图2,在△AEC和△AFB中,
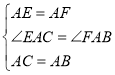 ,
,
∴△AEC≌△AFB(SAS),
∴∠ABF=∠ACE,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠OBC=∠OCB,
∴OB=OC,
又AB=AC,
∴AD垂直平分BC,
故图2正确.

图3,∵AD垂直平分BC,故图3正确.
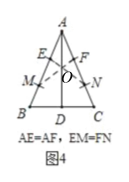
图4,∵AE=AF,EM=FN,
∴AM=AN,
在△AEC和△AFB中,
 ,
,
∴△AEN≌△AFM(SAS),
∴∠ANE=∠AMF,
在△EOM和△FON中,
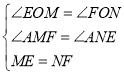 ,
,
∴△EOM≌△FON(AAS),
∴OE=OF,
在△AOE和△AOF中,
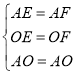 ,
,
∴△AOE≌△AOF(SSS),
∴∠EAO=FAO,
∴AD平分∠BAC,
∴AD⊥BC(三线合一).
故图4正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(a﹣1)x2+2x+a﹣1=0.
(1)若该方程有一根为2,求a的值及方程的另一根;
(2)当a为何值时,方程仅有一个根?求出此时a的值及方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小明从学校到家行进的路程s(米)与时间t(分)的图象,观察图象,从中得到如下信息:①学校离小明家1000米;②小明用了20分钟到家③小明前10分钟走了路程的一半;④小明后10分钟比前10分钟走得快,其中正确的有( )

A. ①②③B. ①②④C. ②③④D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是射线BM上的一个动点(点P不与点B重合),∠AOB= 30°,∠ABM=60°.当∠OAP=______时,以点A、O、B中的任意两点和点P为顶点的三角形是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种电子产品共4件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为
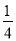 .
.(1)该批产品有正品________件;
(2)如果从中任意取出2件,利用列表或树状图求取出2件都是正品的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
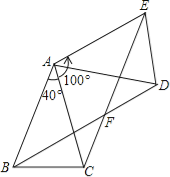
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形.
相关试题

