【题目】一个正多边形的一个内角是135°,则这个正多边形的边数为( )
A.8B.9C.5D.7
参考答案:
【答案】A
【解析】
先根据正多边形的特征求出一外角,然后用360°除以这个外角即可.
解:∵正多边形的一个内角是135°
∴正多边形的每一个外角都是45°
∴正多边形的边数为:360°÷45°=8
故答案为A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P,试说明△EPF为直角三角形.
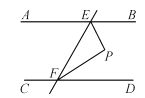
-
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件: , 使得ABCD为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x2﹣4= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】a﹣b 的相反数是______;|3.14﹣π|= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的周长为20cm,现将△ABC沿AB方向平移2cm至△A′B′C′的位置,连接CC′,则四边形AB′C′C的周长是cm.
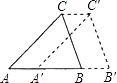
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
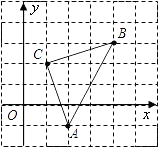
(1)写出点A,B的坐标:
A( , )、B( , )
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′( , )、B′( , )、C′( , ).
(3)△ABC的面积为 .
相关试题

