【题目】如图,在等腰直角△ABC中,∠BAC=90°,AC=AB,以AB为斜边在△ABC内部作Rt△ABD,连接CD,若∠ADC=135°,S△ABD=9,则线段AD的长度为_____.

参考答案:
【答案】3
【解析】
作辅助线,构建三角形AEB,由旋转的性质可得△AED和是等腰直角三角形△BED是等腰直角三角形,设AD=AE=x,则ED=BE=![]() x,BD=
x,BD=![]() x×
x×![]() =2x,根据S△ABD=9,可求得x的值,即AD的长.
=2x,根据S△ABD=9,可求得x的值,即AD的长.
将△ADC绕点A顺时针旋转90°得到△AEB,连接ED,
∴∠EAD=90°,AE=AD,∠AEB=∠ADC=135°,
∴△AED是等腰直角三角形,
∴∠AED=∠ADE=45°,
∴∠BED=135°-45°=90°,
∵∠ADB=90°,
∴∠BDE=45°,
∴△BED是等腰直角三角形,
设AD=AE=x,则ED=BE=![]() x,BD=
x,BD=![]() x×
x×![]() =2x,
=2x,
∵S△ABD=9,
∴![]() ADBD=9,
ADBD=9,
![]() x2x=9,
x2x=9,
x2=9,
x1=3,x2=-3,
∴AD=3,
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,∠BAC=60°,BF,CE为高,点D为BC的中点,连接EF,ED,FD,有下列四个结论:①ED=FD;②∠ABC=60°时,EF∥BC;③BF=2AF;④AF:AB=AE:AC.其中正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个正方体的表面展开图,请回答下列问题:
(1)与面B、C相对的面分别是 ;
(2)若A=a3+a2b+3,B=a2b﹣3,C=a3﹣1,D=﹣(a2b﹣6),且相对两个面所表示的代数式的和都相等,求E、F分别代表的代数式.
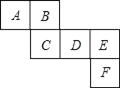
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,已知△ABC三个定点坐标分别为A(﹣4,1),B(﹣3,3),C(﹣1,2).
(1)画出△ABC关于x轴对称的△A1B1C1,点A,B,C的对称点分别是点A1、B1、C1,直接写出点A1,B1,C1的坐标;
(2)画出点C关于y轴的对称点C2,连接C1C2,CC2,C1C,求△CC1C2的面积.
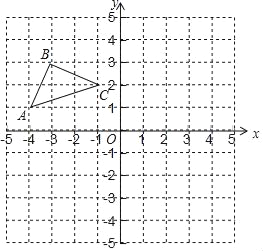
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方形运动场被分隔成
 、
、 、
、 、
、 、
、 共
共 个区,
个区,  区是边长为
区是边长为 的正方形,
的正方形,  区是边长为
区是边长为 的正方形.
的正方形.(1)列式表示每个
 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果
 ,
,  ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?
相关试题

