【题目】如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=![]() CM+
CM+![]() BN.
BN.

参考答案:
【答案】(1)①证明见解析;②80°;(2)证明见解析.
【解析】
试题分析:(1)①通过角的计算找出∠ACD=∠BCE,再结合△ACB和△DCE均为等腰三角形可得出“AC=BC,DC=EC”,利用全等三角形的判定(SAS)即可证出△ACD≌△BCE,由此即可得出结论AD=BE;
②结合①中的△ACD≌△BCE可得出∠ADC=∠BEC,再通过角的计算即可算出∠AEB的度数;
(2)根据等腰三角形的性质结合顶角的度数,即可得出底角的度数,利用(1)的结论,通过解直角三角形即可求出线段AD、DE的长度,二者相加即可证出结论.
试题解析:(1)①证明:∵∠CAB=∠CBA=∠CDE=∠CED=50°,∴∠ACB=∠DCE=180°﹣2×50°=80°.
∵∠ACB=∠ACD+∠DCB,∠DCE=∠DCB+∠BCE,∴∠ACD=∠BCE.
∵△ACB和△DCE均为等腰三角形,∴AC=BC,DC=EC.
在△ACD和△BCE中,∵AC=BC,∠ACD=∠BCE,DC=EC,∴△ACD≌△BCE(SAS),∴AD=BE.
②解:∵△ACD≌△BCE,∴∠ADC=∠BEC.
∵点A,D,E在同一直线上,且∠CDE=50°,∴∠ADC=180°﹣∠CDE=130°,∴∠BEC=130°.
∵∠BEC=∠CED+∠AEB,且∠CED=50°,∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°.
(2)证明:∵△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=120°,∴∠CDM=∠CEM=![]() ×(180°﹣120°)=30°.
×(180°﹣120°)=30°.
∵CM⊥DE,∴∠CMD=90°,DM=EM.
在Rt△CMD中,∠CMD=90°,∠CDM=30°,∴DE=2DM=2×![]() =
=![]() CM.
CM.
∵∠BEC=∠ADC=180°﹣30°=150°,∠BEC=∠CEM+∠AEB,∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°,∴∠BEN=180°﹣120°=60°.
在Rt△BNE中,∠BNE=90°,∠BEN=60°,∴BE=![]() =
=![]() BN.
BN.
∵AD=BE,AE=AD+DE,∴AE=BE+DE=![]() CM+
CM+![]() BN.
BN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的
 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.(1)按原计划完成总任务的
 时,已抢修道路 米;
时,已抢修道路 米;(2)求原计划每小时抢修道路多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】水龙头关闭不严就会滴水,现在没拧紧的水龙头下面放一个容器,容器内的盛水量W(L)与滴水时间t(h)的关系如图所示,给合图象解答下列问题:

(1)容器内原有水多少升?
(2)求W与t之间的函数关系式,并计算在这种滴水状态下一个月(30天)的滴水量是多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
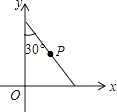
A.(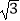 ,1)
,1)
B.(1,﹣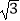 )
)
C.(2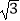 ,﹣2)
,﹣2)
D.(2,﹣2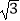 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】随着微电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占为7×10-7平方毫米,这个数用小数表示为()
A. 0.000007 B. 0.000070 C. 0.0000700 D. 0.0000007
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. x2+x3=x6 B. (x3)2=x6 C. 2x+3y=5xy D. x6÷x3=x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2﹣6x+4=0,原方程应变为( )
A.(x+3)2=13B.(x-3)2=5C.(x﹣3)2=13D.(x+3)2=5
相关试题

