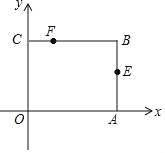
【题目】如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1,若M为x轴上的动点,N为y轴上的动点,则四边形MNFE的周长最小值是_____.
【答案】5+![]()
【解析】
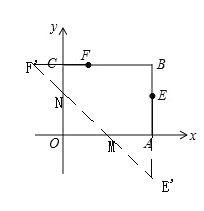
作点E关于x轴的对称点E′,作点F关于y轴的对称点F′,连接E′F′,分别与x轴、y轴交于点M、N,连接FN、NM、ME,此时四边形MNFE的周长最小.根据勾股定理和轴对称性质可求解.
解:由图可得;E(3,1);F(1,2)
如图,作点E关于x轴的对称点E′,作点F关于y轴的对称点F′,连接E′F′,分别与x轴、y轴交于点M、N,连接FN、NM、ME,此时四边形MNFE的周长最小.
∴E′(3,﹣1),F′(﹣1,2),
设直线E′F′的解析式为y=kx+b,
有![]() 解这个方程组,
解这个方程组,
得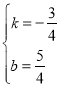
∴直线E′F′的解析式为![]() .
.
当y=0时,x=![]() ,
,
∴M点的坐标为(![]() ,0).
,0).
当x=0时,y=![]() ,
,
∴N点的坐标为(0,![]() ).
).
∵E与E′关于x轴对称,F与F′关于y轴对称,
∴NF=NF′,ME=ME′.F′B=4,E′B=3.
在Rt△BE′F′中,F′E′=![]()
∴FN+NM+ME=F′N+NM+ME′=F′E′=5.
在Rt△BEF中,EF=![]() .
.
∴FN+NM+ME+EF=5+![]() ,
,
即四边形MNFE的周长最小值是5+![]() .
.
故答案为:5+![]()

