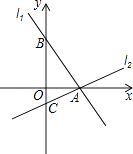
【题目】如图,过点A(2,0)的两条直线l1 , l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB= ![]() .
. 
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.
参考答案:
【答案】
(1)解:∵点A(2,0),AB= ![]()
∴BO= ![]() =
= ![]() =3
=3
∴点B的坐标为(0,3);
(2)解:∵△ABC的面积为4
∴ ![]() ×BC×AO=4
×BC×AO=4
∴ ![]() ×BC×2=4,即BC=4
×BC×2=4,即BC=4
∵BO=3
∴CO=4﹣3=1
∴C(0,﹣1)
设l2的解析式为y=kx+b,则
![]() ,解得
,解得 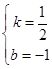
∴l2的解析式为y= ![]() x﹣1
x﹣1
【解析】(1)先根据勾股定理求得BO的长,再写出点B的坐标;(2)先根据△ABC的面积为4,求得CO的长,再根据点A、C的坐标,运用待定系数法求得直线l2的解析式.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A是双曲线
 在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线
在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线 上运动,则k的值是 .
上运动,则k的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1,图2都是8×8的正方形网格,每个小正方形的顶点成为格点,每个小正方形的边长均为1,在每个正方形网格中标注了6个格点,这6个格点简称为标注点
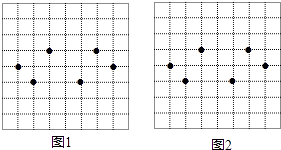
(1)请在图1,图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等);
(2)图1中所画的平行四边形的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】当x=2时,代数式px3+qx+1的值等于2016,那么当x=﹣2时,求px3+qx+1 的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句正确的是( )
A.近似数0.010精确到百分位
B.|x-y|=|y-x|
C.如果两个角互补,那么一个是锐角,一个是钝角
D.若线段AP=BP,则P一定是AB中点
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长是4和9,则等腰三角形的周长为( )
A. 17 B. 17或22 C. 22 D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】地球绕太阳公转的速度约是110000千米/时,将110000用科学记数法表示为( )
A.11×104
B.1.1×105
C.1.1×104
D.0.11×105
相关试题

