Question

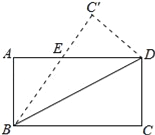
【题目】如图，在矩形ABCD中，BC=6cm，CD=3cm，将△BCD沿BD翻折，点C落在点C′处，BC′交AD于点E，则AE的长为______ cm．

Answer 1

【答案】

【解析】根据翻折的性质可得∠BCD=∠EBD，再根据两直线平行，内错角相等可得∠BCD=∠ADB，从而得到∠EBD=∠ADB，然后根据等角对等边可得BE=DE，再根据矩形的对边相等可得AB=CD，AD=BC，设AE=x，表示出BE，然后在Rt△ABE中，利用勾股定理列出方程求解即可．

解：∵△BCD沿BD翻折，点C落在点C′处，

∴∠BCD=∠EBD，

∵矩形的对边AD∥BC，

∴∠BCD=∠ADB，

∴∠EBD=∠ADB，

∴BE=DE，

在矩形ABCD中，AB=CD=3cm，AD=BC=6cm，

设AE=xcm，则BE=DE=AD﹣AE=6﹣x，

在Rt△ABE中，由勾股定理得，AB2+AE2=BE2，

即32+x2=（6﹣x）2，

解得x=，

即AE=cm．

故答案为： ．

“点睛”本题考查了翻折变换的性质，矩形的性质，平行四边形的性质，等角对等边的性质，难点在于将所求的边以及已知的边的长度转化到同一个直角三角形中利用勾股定理列出方程.