【题目】如图1,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°
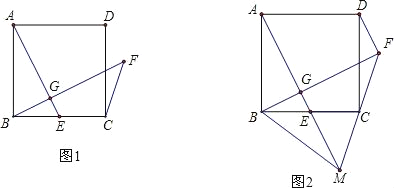
(1)求证:AG=FG;
(2)如图2延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,求FD的长.
参考答案:
【答案】(1)证明见解析;(2)2![]() .
.
【解析】
试题分析:(1)过C点作CH⊥BF于H点,根据已知条件可证明△AGB≌△BHC,所以AG=BH,BG=CH,又因为BH=BG+GH,所以可得BH=HF+GH=FG,进而证明AG=FG;
(2)过D作DQ⊥MF交MF延长线于Q,根据全等三角形的性质和等腰三角形的性质即可求出FD的长.
试题解析:(1)过C点作CH⊥BF于H点,
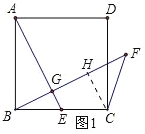
∵∠CFB=45°
∴CH=HF,
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°
∴∠BAG=∠FBE,
∵AG⊥BF,CH⊥BF,
∴∠AGB=∠BHC=90°,
在△AGB和△BHC中,
∵∠AGB=∠BHC,∠BAG=∠HBC,AB=BC,
∴△AGB≌△BHC,
∴AG=BH,BG=CH,
∵BH=BG+GH,
∴BH=HF+GH=FG,
∴AG=FG;
(2)∵CH⊥GF,
∴CH∥GM,
∵C为FM的中点,
∴CH=![]() GM,
GM,
∴BG=![]() GM,
GM,
∵BM=10,
∴BG=2![]() ,GM=4
,GM=4![]() ,
,
∴AG=4![]() ,AB=10,
,AB=10,
∴HF=2![]() ,
,
∴CF=2![]() ×
×![]() =2
=2![]() ,
,
∴CM=2![]() ,
,
过B点作BK⊥CM于K,
∵CK=![]() CM=
CM=![]() CF=
CF=![]() ,
,
∴BK=3![]() ,
,
过D作DQ⊥MF交MF延长线于Q,
∴△BKC≌△CQD
∴CQ=BK=3![]() ,
,
DQ=CK=![]() ,
,
∴QF=3![]() -2
-2![]() =
=![]() ,
,
∴DF=![]() =2
=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2(x+1)<6的解集为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全;
(2)若图中的正方形边长为2cm,长方形的长为3cm,宽为2cm,请直接写出修正后所折叠而成的长方体的体积:__________cm 3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:若
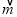 =(a,b),
=(a,b),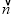 =(c,d),则
=(c,d),则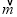 ·
·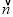 =ac+bd.如
=ac+bd.如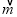 =(1,2),
=(1,2),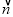 =(3,5),则
=(3,5),则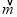 ·
·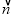 =1×3+2×5=13.
=1×3+2×5=13.(1)已知
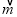 =(2,4),
=(2,4),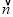 =(2,-3),求
=(2,-3),求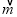 ·
·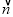 ;
;(2)已知
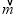 =(x-1,1),
=(x-1,1),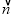 =(x-1,x+1),求y=
=(x-1,x+1),求y=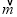 ·
·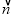 ;
;(3)判断y=
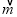 ·
·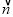 的函数图象与一次函数y=x-1的图象是否相交,请说明理由.
的函数图象与一次函数y=x-1的图象是否相交,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形、菱形、正方形都一定具有的性质是( )
A. 邻边相等 B. 四个角都是直角
C. 对角线相等 D. 对角线互相平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,正方形ABCD的三个顶点坐标分别为A(﹣2,2),B(﹣2,﹣2),C(2,﹣2),则第四个顶点D的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把直线y=3x向下平移2个单位,得到的直线是( )
A. y=3x﹣2B. y=3(x﹣2)C. y=3x+2D. y=3(x+2)
相关试题

