【题目】完成下面的证明过程. 如图,已知∠1+∠2=180°∠B=∠DEF,求证:DE∥BC.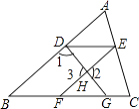
证明:∵∠1+∠2=180°(已知)
∠2=∠3()
∴∠1+∠3=180°
∴∥()
∴∠B=()
∵∠B=∠DEF(已知)
∴∠DEF=()
∴DE∥BC(内错角相等,两直线平行)
参考答案:
【答案】对顶角相等;AB;EF;同旁内角互补,两直线平行;两直线平行,同位角相等;∠CFE;∠CFE;等量代换
【解析】证明:∵∠1+∠2=180°, ∠2=∠3,
∴∠1+∠3=180°
∴AB∥EF,
∴∠B=∠CFE,
∵∠B=∠DEF,
∴∠DEF=∠CFE,
∴DE∥BC.
所以答案是对顶角相等;AB、EF,同旁内角互补,两直线平行;∠CFE,两直线平行,同位角相等;∠CFE,等量代换.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:善于思考的小军在解方程组
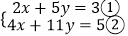 时,采用了一种“整体代换”的解法:
时,采用了一种“整体代换”的解法:
解:将方程②变形:4x+10y+y=5 即2(2x+5y)+y=5③
把方程①带入③得:2×3+y=5,∴y=﹣1
把y=﹣1代入①得x=4,∴方程组的解为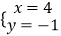 .
.
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组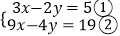
(2)已知x,y满足方程组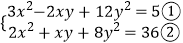 .
.
(i)求x2+4y2的值;
(ii)求 +
+ 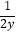 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=
 x与一次函数y=﹣x+7的图象交于点A.
x与一次函数y=﹣x+7的图象交于点A. 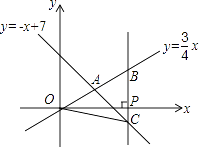
(1)求点A的坐标;
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y= x和y=﹣x+7的图象于点B,C,连接OC.若BC=
x和y=﹣x+7的图象于点B,C,连接OC.若BC= 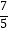 OA,求△OBC的面积.
OA,求△OBC的面积. -
科目: 来源: 题型:
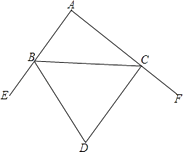
查看答案和解析>>【题目】如图,BD与CD分别平分∠ABC,∠ACB的外角∠EBC,∠FCB,若∠A=80°,则∠BDC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若ab=2,a﹣b=﹣1,则代数式a2b﹣ab2的值等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)计算:
(2)计算:
(3)解方程组: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】添括号:2a-3b-c=2a-(________).
相关试题

