【题目】试解答下列问题:
(1)在图1我们称之为“8字形”,请直接写出∠A,∠B,∠C,∠D之间的数量关系: ;
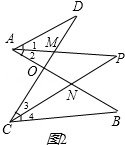
(2)仔细观察,在图2中“8字形”的个数是 个;
(3)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠B与∠P、∠D之间数量关系 .
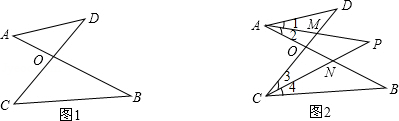
参考答案:
【答案】(1)∠A+∠D=∠C+∠B;(2)6;(3)38°;(4)2∠P=∠D+∠B.
【解析】
试题分析:(1)根据三角形内角和定理即可得出∠A+∠D=∠C+∠B;
(2)根据“8字形”的定义,仔细观察图形即可得出“8字形”共有6个;
(3)先根据“8字形”中的角的规律,可得∠DAP+∠D=∠P+∠DCP①,∠PCB+∠B=∠PAB+∠P②,再根据角平分线的定义,得出∠DAP=∠PAB,∠DCP=∠PCB,将①+②,可得2∠P=∠D+∠B,进而求出∠P的度数;
(4)同(3),根据“8字形”中的角的规律及角平分线的定义,即可得出2∠P=∠D+∠B.
解:(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B;
故答案为:∠A+∠D=∠C+∠B;
(2)①线段AB、CD相交于点O,形成“8字形”;
②线段AN、CM相交于点O,形成“8字形”;
③线段AB、CP相交于点N,形成“8字形”;
④线段AB、CM相交于点O,形成“8字形”;
⑤线段AP、CD相交于点M,形成“8字形”;
⑥线段AN、CD相交于点O,形成“8字形”;
故“8字形”共有6个;
故答案为:6;
(3)∠DAP+∠D=∠P+∠DCP,①
∠PCB+∠B=∠PAB+∠P,②
∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②得:
∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,
即2∠P=∠D+∠B,
又∵∠D=40度,∠B=36度,
∴2∠P=40°+36°,
∴∠P=38°;
(4)关系:2∠P=∠D+∠B.
由∠D+∠1+∠2=∠B+∠3+∠4①
由∠ONC=∠B+∠4=∠P+∠2,②
①+②得:
∠D+2∠B+2∠1+2∠3=∠B+2∠3+2∠P+2∠1,
∠D+2∠B=2∠P+∠B,
即2∠P=∠D+∠B.
故答案为:2∠P=∠D+∠B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,如果抛物线y=3x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系中抛物线的解析式是( )
A. y=3(x﹣2)2+2 B. y=3(x+2)2﹣2
C. y=3(x﹣2)2+2 D. y=3(x+2)2+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ΔABC和ΔDEF中,已知∠C=∠D,∠B=∠E,要判断这两个三角形全等,还需添加条件( )
A. AB=ED B. AB=FD C. AC=FD D. ∠A =∠F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).
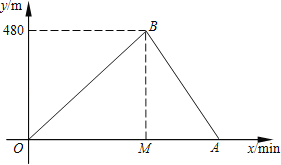
(1)A点所表示的实际意义是 ;
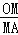 = ;
= ;(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠C=70°,∠B=40°,求∠DAE的度数
(2)若∠C-∠B=30°,则∠DAE=________.
(3)若∠C-∠B=
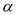 (∠C>∠B),求∠DAE的度数(用含
(∠C>∠B),求∠DAE的度数(用含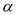 的代数式表示).
的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.
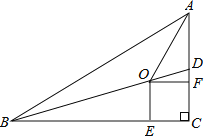
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验表明,人体内某种细胞的形状可近似看作球,它的直径约为0.00000156m,则这个数用科学记数法表示是 m.
相关试题

