【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.

(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
参考答案:
【答案】(1)证明详见解析;(2)AB∥DE,AB=DE,理由详见解析.
【解析】
试题分析:(1)运用AAS证明△ABD≌△CAE;
(2)易证四边形ADCE是矩形,所以AC=DE=AB,也可证四边形ABDE是平行四边形得到AB=DE.
试题解析:证明:(1)∵AB=AC,
∴∠B=∠ACD,
∵AE∥BC,
∴∠EAC=∠ACD,
∴∠B=∠EAC,
∵AD是BC边上的中线,
∴AD⊥BC,
∵CE⊥AE,
∴∠ADC=∠CEA=90°
在△ABD和△CAE中
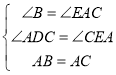
∴△ABD≌△CAE(AAS);
(2)AB∥DE,AB=DE,理由如下:
如图所示,
∵AD⊥BC,AE∥BC,
∴AD⊥AE,
又∵CE⊥AE,
∴四边形ADCE是矩形,
∴AC=DE,
∵AB=AC,
∴AB=DE,
∵AE∥BC,
∴四边形ABDE是平行四边形,
∴AB∥DE,AB=DE.
-
科目: 来源: 题型:
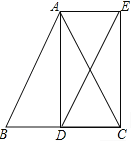
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC,交CD于点F.
(1)、求证:DE=BF;(2)、连接EF,写出图中所有的全等三角形.(不要求证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个条件中,能得到互相垂直关系的有( )
①对顶角的平分线;
②平行线截得的一组同旁内角的平分线;
③平行线截得的一组同位角的平分线;
④平行线截得的一组内错角的平分线.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年刷爆朋友圈的一句小诗:“苔花如米小,也学牡丹开”是央视一台《经典咏流传》节目中的内容.该节目已夺得本年度文化类节目全国网最高的收视率1.33%.下列说法正确的是( )
A. 这个收视率是通过普查获得的
B. 这个收视率是对北京市用等距抽样调查获得的
C. 从全国随机抽取10000户约有133户看了《经典咏流传》
D. 全国平均每10000户约有133户看了《经典咏流传》
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是轴对称图形但不是中心对称图形的是( )
A. 圆B. 平行四边形C. 正六边形D. 等边三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国南宋数学家杨辉曾提出这样一个问题:"直田积(矩形面积),八百六十四(平方步),只云阔(宽)不及长一十二步(宽比长少12步),问阔及长各几步."如果设矩形田地的长为x步,那么同学们列出的下列方程中正确的是 ( )
A.x(x+12)=864 B.x(x-12)=864 C.x2+12x=864 D.x2+12x-864=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条东西走向的马路旁,有青少年宫、学校、商场、医院四家公共场所,已知青少年宫在学校东300m处,商场在学校西200m处,医院在学校东500m处,若将马路近似地看作一条直线,以学校为原点,向东方向为正方向,用1个单位长度表示100m.
(1)在数轴上表示出四家公共场所的位置;
(2)列式计算青少年宫与商场之间的距离.
相关试题

