搜索
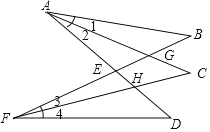
【题目】如图，AC，FC分别平分∠BAD，∠BFD，且分别与FB，AD相交于点G，H，已知∠B=40°，∠D=50°，求∠C的度数．
参考答案：
【答案】45°．
【解析】
由三角形内角和定理得出∠1-∠3=∠C-∠B，同理，∠2-∠4=∠D-∠C，由角平分线定义得出∠1=∠2，∠3=∠4，得出∠C-∠B=∠D-∠C，即可得出∠C的度数．
∵∠B+∠1+∠AGB=180°，∠C+∠3+∠CGF=108°，∠AGB=∠CGF
∴∠B+∠1=∠C+∠3，
∴∠1﹣∠3=∠C﹣∠B，
同理可得：∠2﹣∠4=∠D﹣∠C．
∵AC，FC分别平分∠BAD，∠BFD，
∴∠1=∠2，∠3=∠4，
∴∠C﹣∠B=∠D﹣∠C，
∴∠C
(∠B+∠D)×(40°+50°)=45°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是（ ）
A. 要了解某公司生产的100万只灯泡的使用寿命，可以采用抽样调查的方法
B. 4位同学的数学期末成绩分别为100、95、105、110，则这四位同学数学期末成绩的中位数为100
C. 甲乙两人各自跳远10次，若他们跳远成绩的平均数相同，甲乙跳远成绩的方差分别为0.51和0.62，则乙的表现较甲更稳定
D. 某次抽奖活动中，中奖的概率为
表示每抽奖50次就有一次中奖 -
科目： 来源： 题型：
查看答案和解析>>【题目】设直线y＝kx+6和直线y＝（k+1）x+6（k是正整数）及x轴围成的三角形面积为Sk（k＝1，2，3，…，8），则S1+S2+S3+…+S8的值是（ ）
A.
B.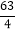 
C. 16D. 14 -
科目： 来源： 题型：
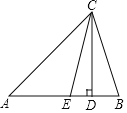
查看答案和解析>>【题目】如图，在△ABC中，CD是AB边上的高，CE是∠ACB的平分线．
（1）若∠A=40°，∠B=76°，求∠DCE的度数；
（2）若∠A=α，∠B=β，求∠DCE的度数(用含α，β的式子表示)；
（3）当线段CD沿DA方向平移时，平移后的线段与线段CE交于G点，与AB交于H点，若∠A=α，∠B=β，求∠HGE与α、β的数量关系．
-
科目： 来源： 题型：
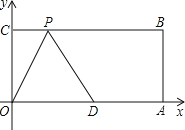
查看答案和解析>>【题目】已知：如图，在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（7，0），C（0，4），点D的坐标为（5，0），点P在BC边上运动. 当△ODP是腰长为5的等腰三角形时，点P的坐标为______________.
-
科目： 来源： 题型：
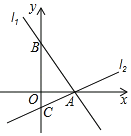
查看答案和解析>>【题目】如图，过点A（4，0）的两条直线l1，l2分别交y轴于点B，C，其中点B在原点上方，点C在原点下方，已知AB＝2
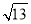．（1）求点B的坐标；
（2）若△ABC的面积为20，求直线l2的解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】学校开展“书香校园”活动以来，受到同学们的广泛关注，学校为了解全校学生课外阅读的情况，随机调查了部分学生在一周内借阅图书的次数，并制成如图不完整的统计表．学生借阅图书的次数统计表
借阅图书的次数
0次
1次
2次
3次
4次及以上
人数
7
13
a
10
3
请你根据统计图表中的信息，解答下列问题：
______，
______．
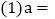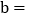该调查统计数据的中位数是______，众数是______．
请计算扇形统计图中“3次”所对应扇形的圆心角的度数；
若该校共有2000名学生，根据调查结果，估计该校学生在一周内借阅图书“4次及以上”的人数．
相关试题
