【题目】学校举办一项小制作评比活动．作品上交时限为3月1日至30日，组委会把同学们交来的作品按时间顺序每5天组成一组，对每一组的作品件数进行统计，绘制成如图所示的统计图．已知从左到右各矩形的高度比为2：3：4：6：4：1．第三组的件数是12．

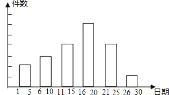
请你回答：（1）、本次活动共有 件作品参赛；各组作品件数的众数是 件；

（2）、经评比，第四组和第六组分别有10件和2件作品获奖，那么你认为这两组中哪个组获奖率较高？为什么？

（3）、小制作评比结束后，组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示，请用树状图或列表法求出刚好展示作品B、D的概率．

参考答案：

【答案】（1）、60；12；（2）、第六组；（3）、.

【解析】

试题分析：（1）、根据第三组的件数和第三组的频率求出总数，得出众数；（2）、首先分别求出第四组和第六组的数量，然后求出获奖率，进行比较大小；（3）、首先画出树状图，然后根据概率的计算法则进行计算.

试题解析：（1）、由题意可得出，本次活动参赛共有：12÷=12÷=60（件），

各组作品件数的众数是12；

（2）、∵第四组有作品：60×=18（件）， 第六组有作品：60×=3（件），

∴第四组的获奖率为：，

第六组的获奖率为：； ∵＜，

∴第六组的获奖率较高；

（3）、画树状图如下：

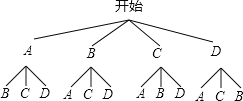
由树状图可知，所有等可能的结果为12种，其中刚好是（B，D）的有2种，

∴刚好展示作品B、D的概率为：P==．

关闭