【题目】如图①,A、B、C、D四点共圆,过点C的切线CE∥BD,与AB的延长线交于点E.
(1)求证:∠BAC=∠CAD;
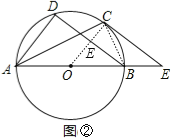
(2)如图②,若AB为⊙O的直径,AD=6,AB=10,求CE的长;
(3)在(2)的条件下,连接BC,求![]() 的值.
的值.

参考答案:
【答案】(1)见解析;(2)CE=![]() ;(3)
;(3)![]() =
=![]() .
.
【解析】
试题分析:(1)连结OC,如图①,根据切线的性质得OC⊥CE,由于CE∥BD,则OC⊥BD,再根据垂径定理得到![]() =
=![]() ,然后利用圆周角定理可得∠BAC=∠CAD;
,然后利用圆周角定理可得∠BAC=∠CAD;
(2)如图②,连结OC交BD于E,由(1)得OC⊥BD,则BE=DE,根据圆周角定理得到∠D=90°,则利用勾股定理可计算出BD=8,所以BE=![]() BD=4,在Rt△OBE中计算出OE=3,再证明△OBE∽△OCE,然后利用相似比可计算出CE的长;
BD=4,在Rt△OBE中计算出OE=3,再证明△OBE∽△OCE,然后利用相似比可计算出CE的长;
(3)先计算出CE=2,由于![]() =
=![]() ,则∠CDB=∠CAB,根据正切定义得到tan∠CBE=
,则∠CDB=∠CAB,根据正切定义得到tan∠CBE=![]() =
=![]() ,则tan∠CBE=
,则tan∠CBE=![]() tan∠CAB=
tan∠CAB=![]() ,即得到
,即得到![]() =
=![]() .
.
(1)证明:连结OC,如图①,
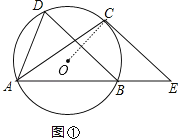
∵CE为切线,
∴OC⊥CE,
∵CE∥BD,
∴OC⊥BD,
∴![]() =
=![]() ,
,
∴∠BAC=∠CAD;
(2)解:如图②,连结OC交BD于E,
由(1)得OC⊥BD,则BE=DE,
∵AB为直径,
∴∠D=90°,
∴BD=![]() =
=![]() =8,
=8,
∴BE=![]() BD=4,
BD=4,
在Rt△OBE中,OE=![]() =3,
=3,
∵BE∥CE,
∴△OBE∽△OCE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CE=![]() ;
;
(3)解:∵OE=3,OC=5,
∴CE=5﹣3=2,
∵![]() =
=![]() ,
,
∴∠CDB=∠CAB,
∵tan∠CBE=![]() =
=![]() =
=![]() ,
,
∴tan∠CAB=tan∠CBE=![]() ,
,
∵tan∠CAB=![]() ,
,
∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
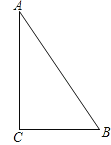
A.AB中点 B.BC中点 C. AC中点 D.∠C的平分线与AB的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( ).
A.弦是直径 B.半圆是弧
C.长度相等的弧是等弧 D.过圆心的线段是直径
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是( )
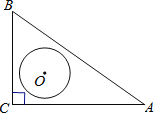
A.r≥1 B.1≤r≤
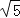 C.1≤r≤
C.1≤r≤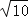 D.1≤r≤4
D.1≤r≤4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,BE⊥AC于E,且D、E分别是AB、AC的中点.延长BC至点F,使CF=CE.

(1)求∠ABC的度数;
(2)求证:BE=FE;
(3)若AB=2,求△CEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)写出数轴上A、B两点表示的数;
(2)动点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒1个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,t为何值时,原点O、与P、Q三点中,有一点恰好是另两点所连线段的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 Rt△ABC中,已知∠C=90°, ∠A=30°,BD是∠B的平分线,AC=18,则BD的值为( )
A. 4.9 B. 9 C. 12 D. 15
相关试题

