【题目】为促进江南新区的发展,長江三桥在区政府的统一指导下夜以继日的修建中,为方便残疾人通行,政府计划在位于南滨路桥头处修建一锲形残疾人通道,如图,该楔形斜坡BC长20米,坡角为12°,区领导为进一步方便残疾人的轮椅车通行,准备把坡角降为5°.

(1)求斜坡新起点到原起点B的距离(精确到0.1米)
(参考数据:sin12°≈0.21,cos12°≈0.98,tan5°≈0.09)
(2)某6人工程队承担这项改进任务(假设每人毎天的工怍效率相同),5天刚好完成该项工程;但实际工作
2天后.有2人因其它工作调离;剩余的工程由余下的4人独自完成,为了不延误工期,每人的工作效率提高了a%,结果准时完成该项工程,求a的值.
参考答案:
【答案】(1)27.1米.(2)a的值是30.
【解析】
试题分析:(1)根据正弦、余弦的定义求出CD、BD的长,根据正切的定义求出AD的长,计算即可;
(2)根据工作效率、工作时间之间的关系列出方程,解方程即可.
解:(1)在Rt△BCD中,CD=BCsin∠CBD=20×0.21=4.2米,
BD=BCcos∠CBD=20×0.98=19.6米,
在Rt△CAD中,AD=![]() ≈46.7米,
≈46.7米,
故斜坡新起点到原起点B的距离AB=AD﹣BD=27.1米.
(2)由题意得:
![]() +
+![]() ×4×(1+a%)=1,
×4×(1+a%)=1,
解得a=30.
答:a的值是30.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(x+y)2﹣x(2y﹣x)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果某一个数的一个平方根是-3,那么这个数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
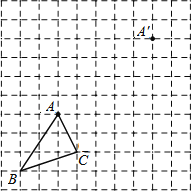
(1)把△ABC平移至A′的位置,使点A与A'对应,得到△A′B′C′;
(2)线段AA′与BB′的关系是: ;
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB于点D,AC=4,BC=3,DB=
 ,
,
(1)、求CD、AD的长
(2)、判断△ABC的形状,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣2与x轴交于A、B两点,与y轴交于点C,已知A(﹣1,0),且tan∠ABC=
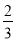 .
.(1)求抛物线的解折式.
(2)在直线BC下方抛物线上一点P,当四边形OCPB的面积取得最大值时,求此时点P的坐标.
(3)在y轴的左侧抛物线上有一点M,满足∠MBA=∠ABC,若点N是直线BC上一点,当△MNB为等腰三角形时,求点N的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的计算正确的是( )
A.8a﹣7a=1
B.2a+3a2=5a3
C.﹣(a﹣b)=﹣a+b
D.2(a﹣b)=2a﹣b
相关试题

